State whether the statements are true or false.If y=∫x0f(t)dt.Thendydt=f(t).
To determine whether the statement "If y=∫x0f(t)dt, then dydt=f(t)" is true or false, we will analyze the problem step by step using the Fundamental Theorem of Calculus.
1. Understand the Definition of y:
We are given that:
y=∫x0f(t)dt
This means y is defined as the integral of the function f(t) from 0 to x.
Hint: Remember that y is a function of x because the upper limit of the integral is x.
2. Differentiate y with respect to x:
To find dydx, we apply the Fundamental Theorem of Calculus, which states that if F(x)=∫xaf(t)dt, then dFdx=f(x).
Therefore, we differentiate y:
dydx=f(x)
Hint: Recall that when differentiating an integral with a variable upper limit, the derivative of the integral is the integrand evaluated at that upper limit.
3. Analyze the Statement:
The statement claims that dydt=f(t). However, we found that:
dydx=f(x)
This indicates that the derivative of y with respect to x is equal to f evaluated at x, not t.
Hint: Pay attention to the variable with respect to which you are differentiating. The notation matters.
4. Conclusion:
Since dydt does not equal f(t) but rather dydx=f(x), the original statement is false.
Final Answer: The statement is False.
We are given that:
y=∫x0f(t)dt
This means y is defined as the integral of the function f(t) from 0 to x.
To find dydx, we apply the Fundamental Theorem of Calculus, which states that if F(x)=∫xaf(t)dt, then dFdx=f(x).
dydx=f(x)
The statement claims that dydt=f(t). However, we found that:
dydx=f(x)
This indicates that the derivative of y with respect to x is equal to f evaluated at x, not t.
Since dydt does not equal f(t) but rather dydx=f(x), the original statement is false.
Topper's Solved these Questions
- Properties and Application of definite IntegralsBook:A DAS GUPTAChapter:Properties and Application of definite IntegralsExercise:EXERCISE
Explore 62 Videos
- Progression, Related Inequalities and SeriesBook:A DAS GUPTAChapter:Progression, Related Inequalities and SeriesExercise:Exercise
Explore 235 Videos
- Recap of Facts and Formulae Book:A DAS GUPTAChapter:Recap of Facts and Formulae Exercise:Exercise
Explore 9 Videos
Similar Questions
Knowledge Check
If f(x)=⎧⎪⎨⎪⎩x,0≤x≤12−ex−1,1<x≤2x−e,2<x≤3 and g'(x)=f(x),x∈[1,3], then
Ag(x) has local minima at x = e and local maxima at x = 1 + ln 2Bg(x) has local maxima at x = 1 and local minima at x = 2Cg(x) does not have local maximaDg(x) does not have local minima
State whether the statements are true (T) or (F) false.
All kites are squares.
View Solutionstate whether the statement are true (T) or false (F).
 is a concave polygon.
is a concave polygon.
View SolutionState whether the statements are true (T) or (F) false.
A kite is not a convex quadrilateral.
View SolutionState whether the statements are true (T) or (F) false.
Diagonals of a rectangle are equal.
View Solutionstate whether the statement are true (T) or false (F).
Every kite is a trapezium.
View SolutionState whether the statements are true (T) or (F) false.
Every rhombus is a trapezium.
View Solutionstate whether the statement are true (T) or false (F).
 is a simple closed curve.
is a simple closed curve.
View Solution
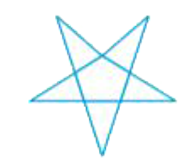 is a polygon.
is a polygon. is a concave pentagon.
is a concave pentagon.