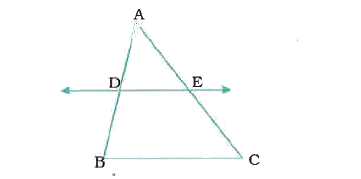
If a line intersects sides AB and AC of a △ABC at D and E respectively and is parallel to BC, prove that ADAB=AEAC (see the given figure).
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:ADAB=AEAC
Step by step video, text & image solution for If a line intersects sides AB and AC of a triangleABC at D and E respectively and is parallel to BC, prove that (AD)/(AB)=(AE)/(AC) (see the given figure). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
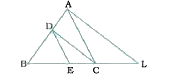
In the given figure, CD||LA and DE||AC. Find the length of CL if BE= 4 cm and EC= 2 cm.
View SolutionFill in the blanks using the correct word given in brackets :
All circles are………(congruent, similar)
View SolutionThe slant height of a frustum of a cone is 4 m and the perimeter of circular ends are 18 m and 16 m. Find the cost of painting its curved surface at 10 per sq. m.
View SolutionIf a line intersects sides AB and AC of a ΔABCat D and E respectively and is parallel to BC, prove that ADAB=AEAC
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn the figure (not to scale) AB = AC and BD = CD. Find ∠ADB
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C15_E05_003_Q01.png" width="80%"gt
View Solution
