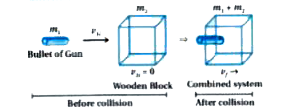
Discuss the completely inelastic collision in one dimension .
 Solution in Gujrati
Solution in Gujrati
Here particle of mass m1 is moving speed v1f in x direction .
∴θ1=θ2=0
From the law of conservation of momentum , momentum before collision and momentum after collision is same .
∴M1v1f=(m1+m2)v1f ...(1)
Energy is dissipated during collision , ΔK = kinetic energy before collision - kinetic energy after collision
12m1v21i−12(m1+m2)v2f [∴v2i=0]
Substituting the value of equation (1) ,
ΔK=12m1v21i−12(m1+m2)×(m1m1+m2)2v21i
=12m1v21i[1−m1m1+m2]
∴ΔK=12m1m2v21i is positive .
Note If particles moves in the same direction and speed of particle of mass m1v1i and if v1i>v2i them , after inelastic both having speed vf
vf=m1v1i+m2v2im1+m2
Kinetic energy before collision ,
Ki=12m1v21i+12m2v22i
Kinetic energy after collision ,
Kf=12(m1+m2)v2f
∴Kf=12(m1+m2)(m1v1i+m2v2i)2(m1+m2)2
=12(m1v1i+m2v2i)2(m1+m2)
∴ Energy dissipated after collision ,
Ki−Kf=12m1v21i+12m2v22i
−12(−m1v1i+m2v2i)2m1+m2
{m21v21i+m1m2v22i+m1m2v21i+m22v22i=12}(−m21v21i+2m1m2v1iv2i+m22v22i(m1+m2))
m1m2v22i+m1m2v21i=12(−2m1m2v1iv2i+v22i)m1+m2
=m1m22(m1+m2)(v21i−2v21i−2v1iv2i+v22i)
=m1m22(m1+m2)(v21i−2v1iv2i+v22i)
=m1m22(m1+m2)[v1i−v2i]2.
Hence ,kinetic energy is conserved in inelastic collision .
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - A Questions - Answers (Try Yourself (VSQs))
74 Videos
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - B Numericals (Numerical From Textual Illustration)
29 Videos
- WAVESBOOK - KUMAR PRAKASHANCHAPTER - WAVESEXERCISE - SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)
23 Videos
Similar Questions
Define the scalar product of two vectors .
View SolutionFind the angle between force →F=(3ˆi+4ˆj−5ˆk) unit and displacement →d=(5ˆi+4ˆj+3ˆk) unit , Also find the projection of F on d .
View SolutionIn a standing wave formed by two atoms separated by 1.21Å, there are 3 nodes and 2 antinodes. Find its wavelength.
View SolutionDiscuss briefly inelastic collisions in one dimension.
View SolutionA completely inelastic collision is one in which the two colliding particles
View SolutionArrive at an expression for elastic collision in Dimension and discuss various case.
View SolutionPerfectly Inelastic Collision In 1-Dimension
View SolutionDiscuss briefly the elastic collision in one dimension . Also , analyse their special cases .
View SolutionCollisions|Perfectly Inelastic Collisions In One Dimension
View SolutionFor complete inelastic collision, restitution coefficient e = …...
View SolutionDiscuss elastic collision in two dimensions. What are the conditions of glancing collision
View SolutionDefine the terms Elastic collision and Inelastic collision. What is the difference between an inelastic collision and a completely inelastic collision ?
View SolutionWhich of the following is an example of completely inelastic collision
View SolutionWhich of the following is an example of completely inelastic collision
View SolutionA completely inelastic collision is one in which the two colliding particles
View Solution
