A rocket accelerates straight up by ejecting gas downwards . In small time interval Δt , it ejects a gas of mass Δm at a relative speed u . Calculate kE of the entire system at t+Δtandt and show that the device that ejects gas does work = (12)Δmu2 in this time interval (negative gravity ).Solution in Gujrati
M =mass of rocket at t
v = velocity of rocket at t
Δm = mass of ejected gas in Δt
u = relative speed of ejected gas
Consider at time t + Δt
(KE)t+(KE)Δt=KE of rocket + Ke of =12(M−Δm)(v+Δv)2+12Δm(v−u)2
12Mv2+MvΔv−Δmvu+12Δmu2
(KE)t= KE of the rocket at time t = 12Mv2
ΔK−(KE)t+(KE)Δt−(KE)t
(MΔv−Δmu)v+12Δ mu2
Hene , Mdvdt=dcdt|u|
∴MΔv=Δmu
∴ΔK=12Δmu2
Now , by work - energy theorem ,
ΔK=ΔW
∴ΔW=12Δmu2
Topper's Solved these Questions
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - E Multiple Choice Questions (MCQs)
64 Videos
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - F Questions From Module (Sample questions for preparation of competitive exams)
23 Videos
- WORK, ENERGY AND POWER BOOK - KUMAR PRAKASHANCHAPTER - WORK, ENERGY AND POWER EXERCISE - SECTION - D NCERT Exemplar Solutions (Short Answer Type Questions)
10 Videos
- WAVESBOOK - KUMAR PRAKASHANCHAPTER - WAVESEXERCISE - SECTION-F (Questions From Module) (Sample questions for preparation of competitive exams)
23 Videos
Similar Questions
The potential energy of 1 kg particle , free to move allong is given by U(x)=(x33−x22)I. if its mechanical energy is 2J . Its maximum speed is …… ms−1
View SolutionA Sphere makes an inslastic collision with another sphere of same mass , then both the spheres are moving .The angle between their direction of motion will be ……..
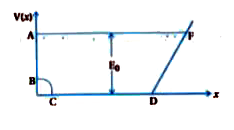
View SolutionA graph of potential energy V(x) verses x is shown in figure .A particle of energy E0 is executing motion in it . Draw graph of velocity and kinetic energy verses x for one complete cycle AFA.
View SolutionIn a standing wave formed by two atoms separated by 1.21Å, there are 3 nodes and 2 antinodes. Find its wavelength.
View SolutionAt a certant of time the mass of a roket going up vertically is 100kg. If it is ejecting 5kg of gas per second at a speed of 400m//s , the acceleration of the rocket would be ("talking" g=10m//s^(2))
View SolutionA rocket accelerates straight up by ejecting gas downwards. In a small time interval Deltat , it ejects a gas of mass Delta m at a relative speed u . Calculate KE of the entire system at t+Deltat and t and show that the device that ejects gas does work =((1)/(2))Delta m . u^(2) in this time interval (neglect gavity).
View SolutionA 5000 kg rocket is set for verticle firing the relative speed of burnt gas is 800ms^(-1) To give an initial upwards acceleration of 20ms^(-2) the amount of gas ejected per second to supply the needed thrust will be
View SolutionA 500 kg rocket is set of vertical firing. The relative speed of burnt gas is 800ms^(-1) To give an initial upwards acceleration of 20ms^(-2) , the amount of gas ejected per second to supply the needed thrust will be
View SolutionSuppose a rocket with an intial mass M0 eject a mass Δm in the form of gases in time Δt, then the mass of the rocket after time t is :-
View SolutionIf rocket engine ejects fuel at the rate mu kg/s with relative velocity v_(r) . At time t = 0, speed of rocket is u. Consider the value of acceleration due to gravity is constant and equal to g. Find velocity of rocket as function of time.
View SolutionIf rocket engine ejects fuel at the rate μ kg/s with relative velocity vr. At time t = 0, speed of rocket is u. Consider the value of acceleration due to gravity is constant and equal to g.
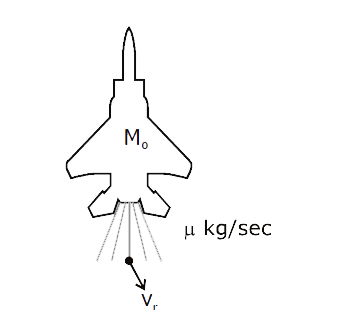
If rocket is in gravity free space then find velocity of rocket as function of time.
View SolutionIn the reaction A→B , if the change in concentration of A in the time interval Δt is Δ[A] , then the rate of reaction is −Δ[A]Δt . What is the significance of the 'negative ' sign in the expression −Δ[A]Δt ?
View SolutionA rocket in space is being propelled by the ejection of a gas. What is the velocity of the centre of mass of the rocket-fuel system?
View SolutionA rocket burns 50g of fuel per second ejecting it as a gas with a velocity of 5 xx 10 cm s^(-1) . What force is exerted by the gas on the rocket?
View SolutionA rocket accelerates straight up by ejecting gas downwards. In a small time interval Δt, it ejects a gas of mass Δm at a relative speed u . Calculate KE of the entire system at t+Δt and t and show that the device that ejects gas does work =(12)Δm.u2 in this time interval (neglect gavity).
View Solution
