Particles of masses m1 and m2 are at a fixed distance apart. If the gravitational field strength at m1 and m2 are →I1 and →I2 respectively.
m1→I1+m2→I2=0
m1→I2+m2→I1=0
m1→I1−m2→I2=0
m1→I2−m2→I1=0
The correct Answer is:A
Topper's Solved these Questions
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -1B
46 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II) PRACTICE SHEET (ADVANCED)Integer Type Questions
6 Videos
- HORIZONTAL CIRCULAR MOTIONBOOK - AAKASH SERIESCHAPTER - HORIZONTAL CIRCULAR MOTIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) Integer Type Questions)
3 Videos
Similar Questions
Assertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1
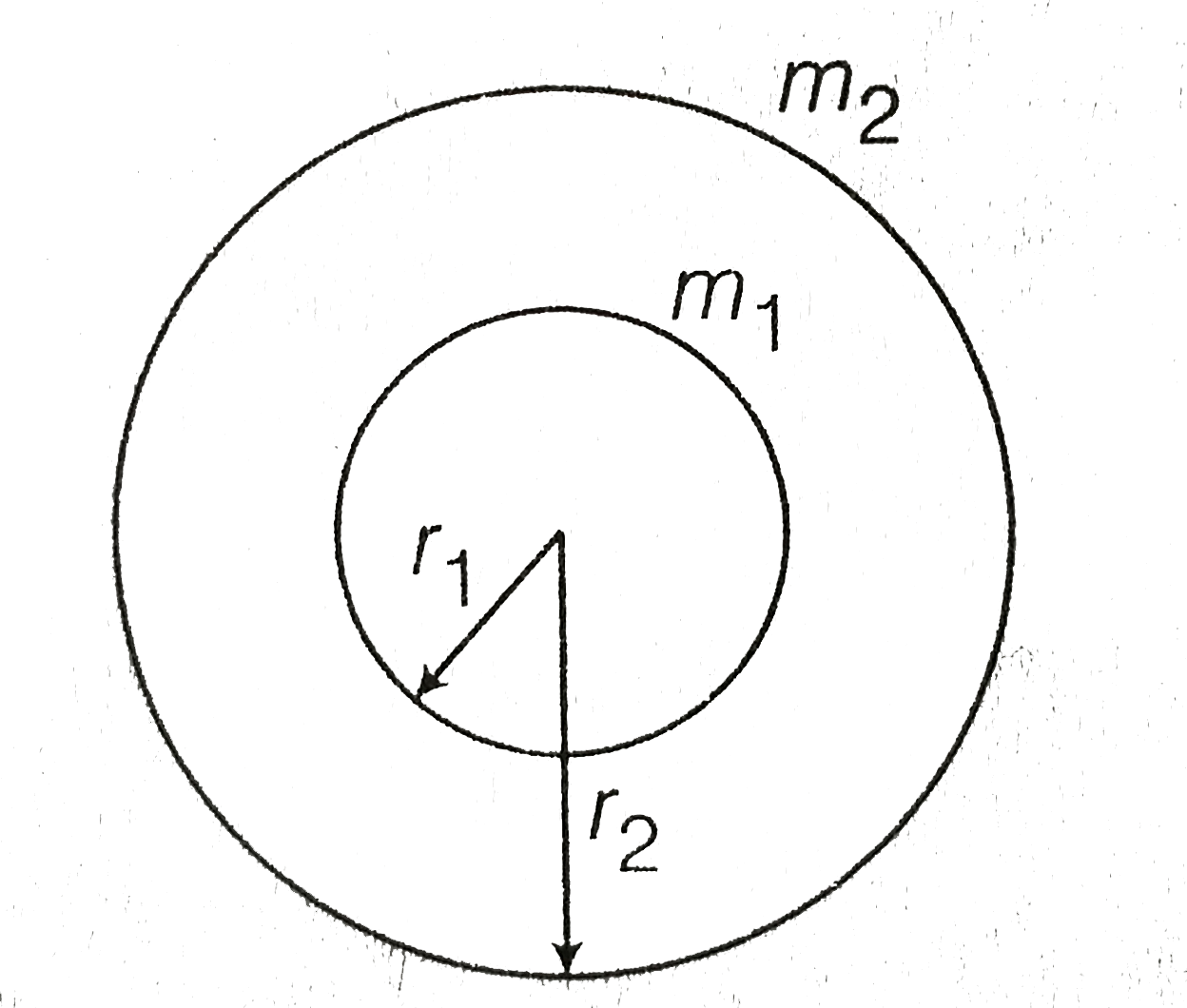
Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).
View SolutionTwo bodies of masses m1 and m2 are placed at a distance r apart. Show that the position where the gravitational field due to them is zero, the potential is given by
−G(m1+m2+2√m1+m2)/r
View Solution
Knowledge Check
Particles of masses m1 and m2 are at a fixed distance apart. If the gravitational field strength at m1 and m2 are →I1 and →I2 respectively. Then
Am1→I1+m2→I2=0Bm1→I2+m2→I1=0Cm1→I1−m2→I2=0Dm1→I2−m2→I1=0Two like poles of strengths m1 and m2 are at far distance apart. The energy repuired to bring them r0 distance apart is
A(μ04πm1m2r0)B(μ08πm1m2r0)C(μ016πm1m2r0)D(μ02πm1m2r0)Assertion : Two spherical shells have masses m1andm2. Their radii are r1andr2. Let r be the distance of a point from centre. Then gravitational field strength and gravitational potential both are equal to zero for O<r<r1

Reason : In the region r1<r<r2, gravitational field strength due to m2 is zero. But gravitational potential due to m2 is constant (but non-zero).AIf both Assertin and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are correct but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is falseDIf Assertion is false but Reason is true
Two bodies of masses m1andm2 ar placed at a distance r apart. Shows that the position where the gravitational field due to them is zer, the potential is given by
V=−Gr[m1+m2+2√m1m2]
View SolutionTwo bodies of masses m1 and m2 are placed distant d apart. Show that the position where the gravitational field due to them is zero, the potential is given by, V=−Gd(m1+m2+2√m1m2)
View SolutionThe gravitational force between two particles of masses m1 and m2 separeted by the same distance, then the gravitational force between them will be
View SolutionTwo bodies of masses M1 and M2, are placed at a distance R apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
View SolutionTwo masses m1 and m2(m1<m2) are released from rest finite distance. They start under their mutual gravitational attraction-
View Solution
