Question

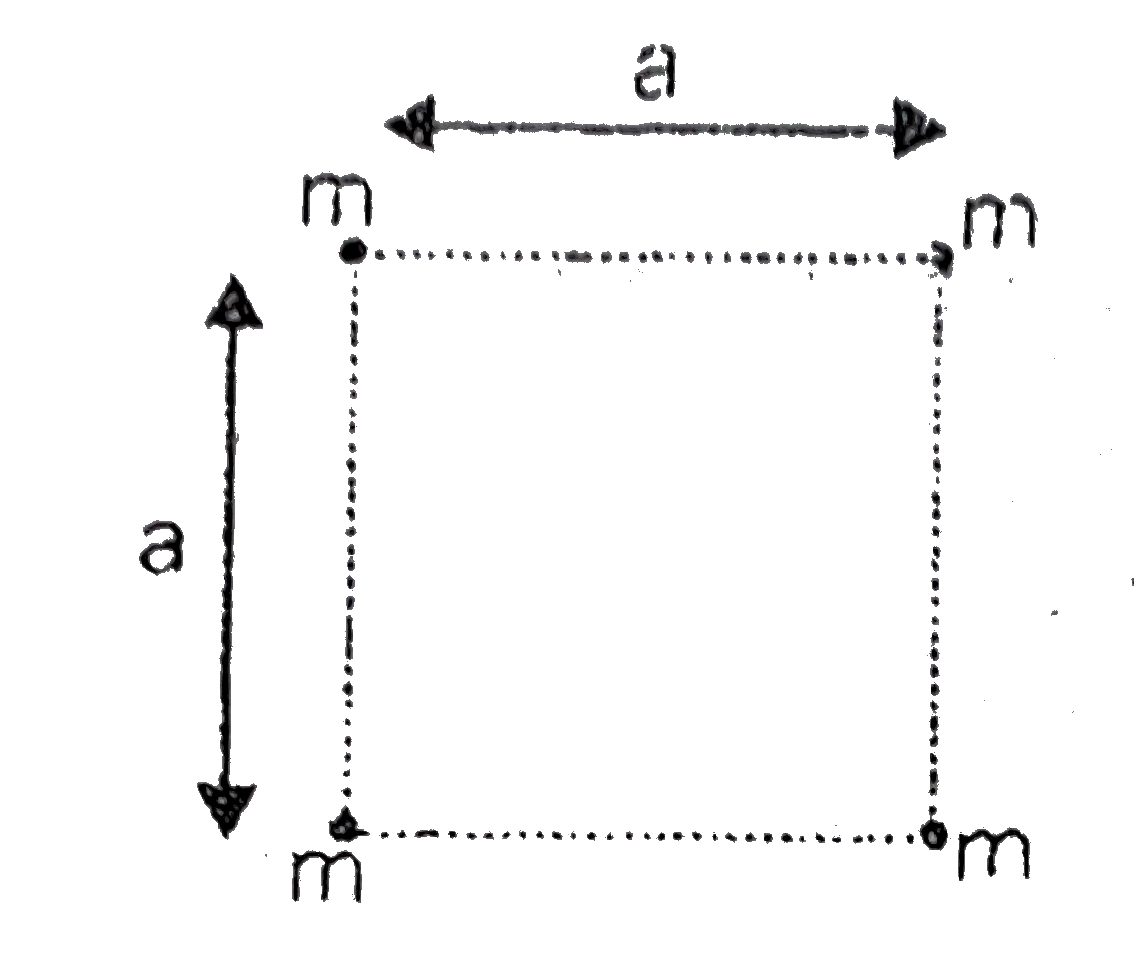
Four particles each of mass 'm' are located at the four corners of a sqaure of side 'a'. If the system is revolving in a uniform circle due to there is mutual force if attraction, then the angular velocity of each particle is

Options

A. `sqrt((Gm(2sqrt(2)+1))/(a^(3)))`
B. `sqrt((Gm)/(a^(3))(sqrt(2)+1))`
C. `sqrt((Gm)/(a^(3))(sqrt(2)+(1)/(2)))`
D. `sqrt((Gm)/(a^(3))(2+(1)/(sqrt(2))))`

Answer

D