The potential energy of a particle varies with distance x from a fixed origin as where A and B are constants. The dinmensions of AB are Solution in Telugu
The correct Answer is:D
Step by step video, text & image solution for The potential energy of a particle varies with distance x from a fixed origin as V = (Asqrt(x))/(x+B) where A and B are constants. The dinmensions of AB are by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - UNITS AND MEASUREMNET (MEASUREMENT OF ERRORS)66videos
RIVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - UNITS AND MEASUREMNET (SIGNIFICANT FIGURES AND ROUNDING OFF)34videos
RIVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - RIVISION EXERCISEEXERCISE - UNITS AND MEASUREMNET (DERIVING THE EQUATIONS)22videos
RIVISION EXERCISE
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICS EXERCISE - EXERCISE III64videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - ROTATIONAL DYNAMICS EXERCISE - PRACTICE SHEET (ADVANCED) Integer Type Questions7videos
ROTATIONAL DYNAMICS
Similar Questions
Measurement of errors 35. The length of a rectangular plate is measured as 10 cm by a vernier scale of least count 0.01 cm and its breadth as 5 cm by the same scale. The percentage error in area is
02:35View SolutionThe radius of a sphere is 6.01 cm. Its volume to four significant figures is
View SolutionIf pressure P, velocity of light C and acceleration due to gravity g are chosen as fundamental units, then dimensional formula of mass is
03:12View SolutionTwo plane mirrors are arranged at right angles to each other as shown in figure. A ray of light is incident on the horizontal mirror at an angle θ For what value of θ the ray emerges parallel to the incoming ray after reflection from the vertical mirror?
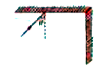 04:50View Solution
04:50View SolutionFour uniform solid spheres each of diameter √5 cm and mass 0.5 kg are placed with their centres at the corners of a square of side 4 cm. The moment of inertia of the system about the diagonal of the square is N×10−4kg m2, then the value of N is .
03:54View SolutionThe potential energy of a particle varies with distance x from a fixed origin as U = (A sqrt(x))/( x^(2) + B) , where A and B are dimensional constants , then find the dimensional formula for AB .
03:54View SolutionThe potential energy 'U' of a particle veries with distance 'x' from a fixed origin as U=AXx2+B. Where A and B are dimensional constants. Find the dimension of length in AB.
View SolutionThe potential energy of a particle varies with distance x from a fixed origin as V= (Asqrt(X))/(X + B) where A and B are constants . The dimension of AB are
View SolutionThe potential energy U of a particle varies with its distance x from a predefined origin as U =A√xx+B, where A and B are constants . Find out the dimension of the quantity AB.
04:24View SolutionThe potential energy of a particle varies with distance x from a fixed origin as V = (Asqrt(x))/(x+B) where A and B are constants. The dinmensions of AB are
02:23View SolutionThe potential energy of a particle varies with distance x from a fixed origin as V=A√xx+B where A and B are constants. The dinmensions of AB are
View SolutionThe potential energy U of a particle varies with distance x from a fixed origin as U=A√xx2+B where A and B are dimensional constants. The dimensional formula for AB is
View SolutionThe potential energy of a particle varies with distance x from a fixed origin as V=A√xx+B where A and B are constants. The dimensions of AB are
03:21View SolutionThe potential energy of a particle varies with distance x from a fixed origin as U = (A sqrt(x))/( x^(2) + B) , where A and B are dimensional constants , then find the dimensional formula for AB .
03:48View SolutionThe potential energy of a particle varies with distance x from a fixed origin as U=A√xx2+B, where AandB are dimensional constants , then find the dimensional formula for AB.
02:37View Solution

