The relation between P and T for monoatomic gas during adiabatic process is P∝TC. The value of C is
5/2
2/5
5/3
3/5
The correct Answer is:A
Similar Questions
The relation between U, p and V for an ideal gas in an adiabatic process is given by relation U=a+bpV. Find the value of adiabatic exponent (γ) of this gas.
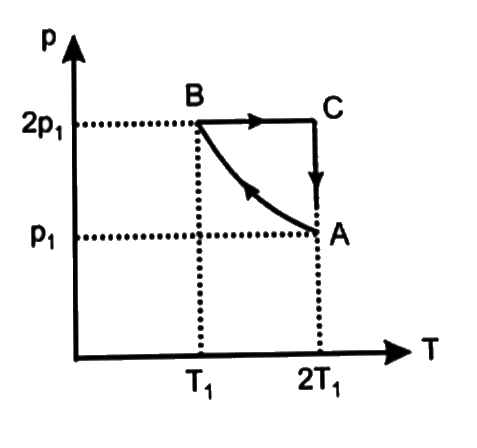
View SolutionTwo moles of an ideal monoatomic gas is taken through a cycle ABCA as shown in the p - T diagram. During the process AB, the pressure and temperature of the gas vary such that pT = constant. If T1=300K and the amount of heat released by the gas during the process AB is Q=−xR, then the value of x is
View Solution
Knowledge Check
The adiabatic relation between P and T is
AP1−γ.Tγ= constantBPTγ= constantCPγT1−γ= constantDPγTγ−1= constantThe relation between U,P and V for an ideal gas in an adiabatic process is given by U = 2 + 3 PV. The gas is
AmonoatomicBdiatomicCpolyatomicDeither monoatomic or diatomicThe relation between U, p and V for an ideal gas in an adiabatic process is given by relation U=a+bpV. Find the value of adiabatic exponent (γ) of this gas.
Ab+1bBb+1aCa+1bDaa+b
Two moles of an ideal monoatomic gas is taken through a cycle ABCA as shown in the p - T diagram. During the process AB, the pressure and temperature of the gas vary such that pT = constant. If T1=300K and the amount of heat released by the gas during the process AB is Q=−xR, then the value of x is

View SolutionIn an adiabatic change, the pressure and temperature of a monoatomic gas are related with relation as P∝TC, Where C is equal to:
View SolutionIn an adiabatic change the pressure and temperature of monoatomic gas are related as P∝Tc where C equal
View SolutionIn an adiabatic change, the pressure and temperature of a monoatomic gas are related with relation as P∝TC, Where C is equal to:
View SolutionThe temperature of an ideal gas undergoing adiabatic expansion varies with volume as T∝V−34, then the value of CPCV for the gas is
View Solution
