F=Gm1m2r2 is valid
Between bodies with any shape
Between particles
Between any bodies with uniform density
Between any bodies with same shape
The correct Answer is:C
Topper's Solved these Questions
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -1B
46 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE-2
146 Videos
- GRAVITATIONALBOOK - AAKASH SERIESCHAPTER - GRAVITATIONALEXERCISE - EXERCISE -3
154 Videos
- GRAVITATIONBOOK - AAKASH SERIESCHAPTER - GRAVITATIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II) PRACTICE SHEET (ADVANCED)Integer Type Questions
6 Videos
- HORIZONTAL CIRCULAR MOTIONBOOK - AAKASH SERIESCHAPTER - HORIZONTAL CIRCULAR MOTIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) Integer Type Questions)
3 Videos
Similar Questions
Assertion : Mass of the rod AB is m1 and of particle P is m2. Distance between centre of rod and particle is r. Then the gravitational force between the rod and the particle is
F=Gm1m2r2
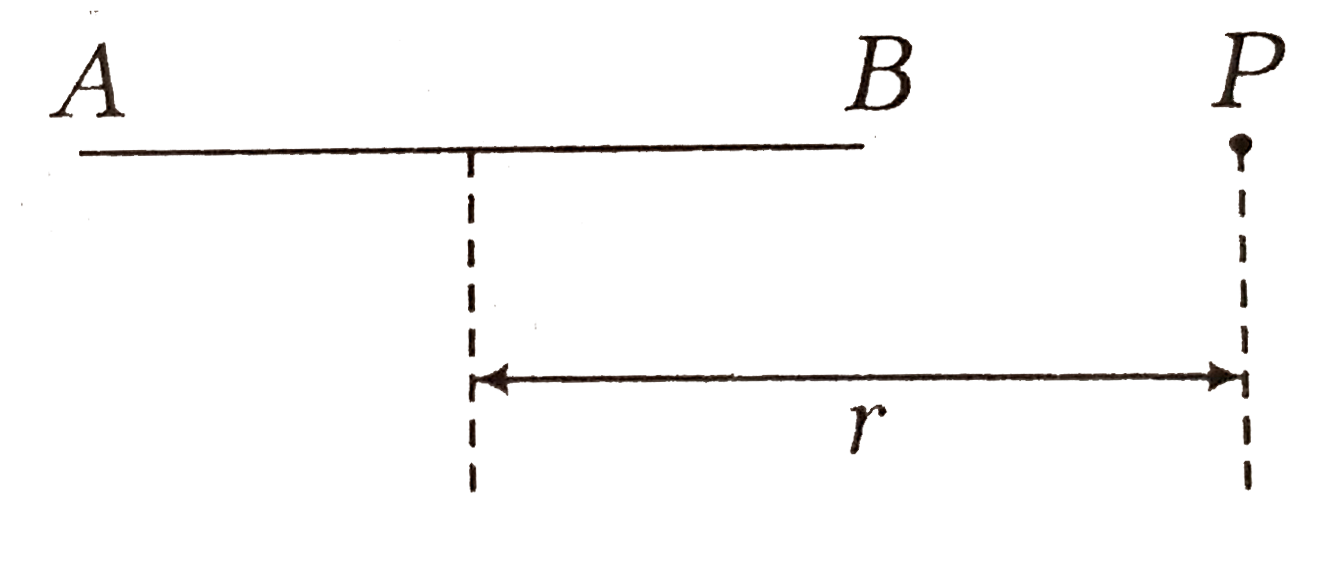
Reason : The relation F=Gm1m2r2 can be applied directly only to find force between two particles.
View SolutionFind the dimensional formula of the following question :
(a) Surface tension T
(b) Universal constant of gravitation , G
(c ) Impulse ,J
(d) Torque τ
The equation involving these equations are :
T=FilF=Gm1m2r2,J=F×t and τ=F×1
View Solution
Knowledge Check
Assertion : Mass of the rod AB is m1 and of particle P is m2. Distance between centre of rod and particle is r. Then the gravitational force between the rod and the particle is
F=Gm1m2r2

Reason : The relation F=Gm1m2r2 can be applied directly only to find force between two particles.AIf both Assertin and Reason are correct and Reason is the correct explanation of AssertionBIf both Assertion and Reason are correct but Reason is not the correct explanation of AssertionCIf Assertion is true but Reason is falseDIf Assertion is false but Reason is trueThe gravitational force F between two masses m1andm2 separeted by a distance r is given by
F=Gm1m2r2
Where G is the universal gravitational constant. What are the dimensions of G ?AM−1L2T−3BM−1L3T−2CML3T−2DML2T−3Which one of the following statements is true for the relation F=Gm1m2r2? (All symbols have their usual meanings)
AThe quantity G depends on the local value of g, acceleration due to gravity.BThe quantity G is greatest at the surface of the EarthCThe quantity G is used only when earth is one of the two massesDThe quantity G is a universal constant
Find the dimensional formula of the following question :
(a) Surface tension T
(b) Universal constant of gravitation , G
(c ) Impulse ,J
(d) Torque τ
The equation involving these equations are :
T=FilF=Gm1m2r2,J=F×t and τ=F×1
View SolutionAccording to Newton's law of gravitational, everybody in this universe attracts every other body with a force, which is directly proportional to the product of their masses and is inversely proportional to the square of the distance between their centres, i.e.,
F∝m1m2r2 or F=Gm1m2r2
where G is universal gravitational constant =6.67×10−11Nm2kg−2.
(i) What is the value of G on the surface of moon?
(ii) How is the gravitational force between two bodies affected when distance between them is halved?
(iii) What values of like do you learn from this law?
View SolutionCheck the dimensional consistency of the equation mV2r=Gm1m2r2.
View SolutionAssertion : The centres of two cubes of masses m1andm2 are separated by a distance r. The gravitational force between these two cubes will be Gm1m2r2
Reason : According to Newton's law of gravitation, gravitational force between two point masses m1andm2 separated by a distance r is Gm1m2r2.
View SolutionAssertion : The centres of two cubes of masses m1andm2 are separated by a distance r. The gravitational force between these two cubes will be Gm1m2r2
Reason : According to Newton's law of gravitation, gravitational force between two point masses m1andm2 separated by a distance r is Gm1m2r2.
View Solution
