A small mass m is moved slowly from the surface of the earth to a height h above the surface. The work done (by an external agent) in doing this is
(a) mgh for all values of h
(b) mgh, for $h < < R$
(c) $\frac{1}{2} m g R$ , for h = R
(d) $- \frac{1}{2} m g R$ , for h = R

only a & b are true s

only b & c are true

only a & d are true

all are true

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

A geostationary satellite is at a height $h$ above the surface of earth. If earth radius is $R$ -

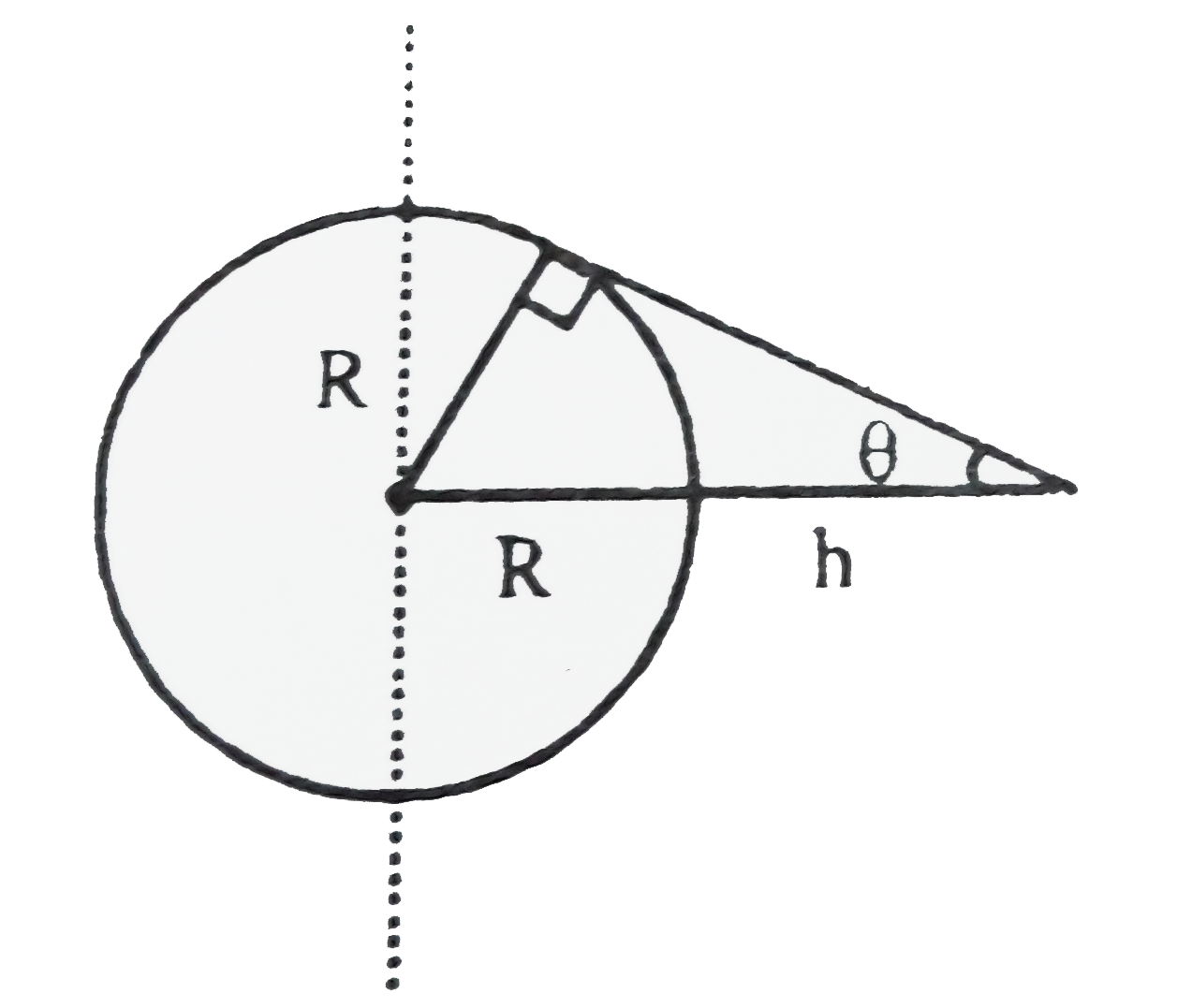AThe minimum colatitude on earth upto which the satellite can be used for communication is ${sin}^{- 1} (R / R + h)$
BThe maximum colatitudes on earth upto which the satellite can be used for communication is ${sin}^{- 1} (R / R + h)$
CThe area on earth escaped from this satellite is given as $(2 π R^{2} (1 + sin θ))$
DThe area on earth escaped from this satellite is given as $(2 π R^{2} (1 + cos θ)$
If the potential energy of a body at a height h from the surface of the earth is $\frac{m g R}{2}$ , then
Ah = 2R
B $h = \frac{R}{2}$
C $h = \frac{R}{3}$
Dh = R
The ratio of accleration due to gravity at a depth h below the surface of earth and at a height h above the surface of earth for h $< <$ radius of earth:
AIs constant
BChanges linearly with h
CChanges parabolically with h
DDecreases