If a pendulum has significant amplitude (up to a factor of 1/e of original) only in the period between t=0s to t=Tsec, then T may be called the average life of the pendulum. When the spherical bob of the pendulum of mass 1kg suffers a retardation (due to viscos drag) proportional to into velocity with 'b' as the constant of proportionally, the average life time of pendulum is (assuming damping is small) in seconds.
0.693b
b
1b
2b
The correct Answer is:D
Similar Questions
If a simple pendulum has significant amplitude (up to a factor of 1e of orginal) only in the period between t=0 sec to t=τ sec, then τ may be called the average life of pendulum. When the spherical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity, with 'b' as the constant of proportionality, the average life time of the pendulum is (assuming damping is small) in seconds:
View SolutionA simple pendulum of length L has a period T. If length is changed by ΔL, the change in period ΔT is proportional to
View Solution
Knowledge Check
If a simple pendulum has significant amplitude (up to a factor of 1/e of original) only in the period between t = Os to t=τs, then τ may be called the average life of the pendulum. When the spherical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity, with 'b' as the constant of proportionality, the average life time of the pendulum is (assuming damping is small) in seconds:
A(a) (0.693)/bB(b) bC(c )1bD(d) 2bA simple pendulum is set into vibrations. The bob of the pendulum comes to rest after some time due t
AAir frictionBMoment of inertiaCweight of the bobDCombination of all the aboveIf T and T' are the periods of a simple pendulum and a conical pendulum of the sample length then .
AT=T'BT<T'CT>T'DT=12T'
Derive an expression for the time period (T) of a simple pendulum which may depend upon the mass (m) of the bob, length (l) of the pendulum and acceleration due to gravity (g).
View SolutionIf the time period of a pendulum is 1sec, then what is the length of the pendulum at point of intersection of l−T and l−T2 graph.
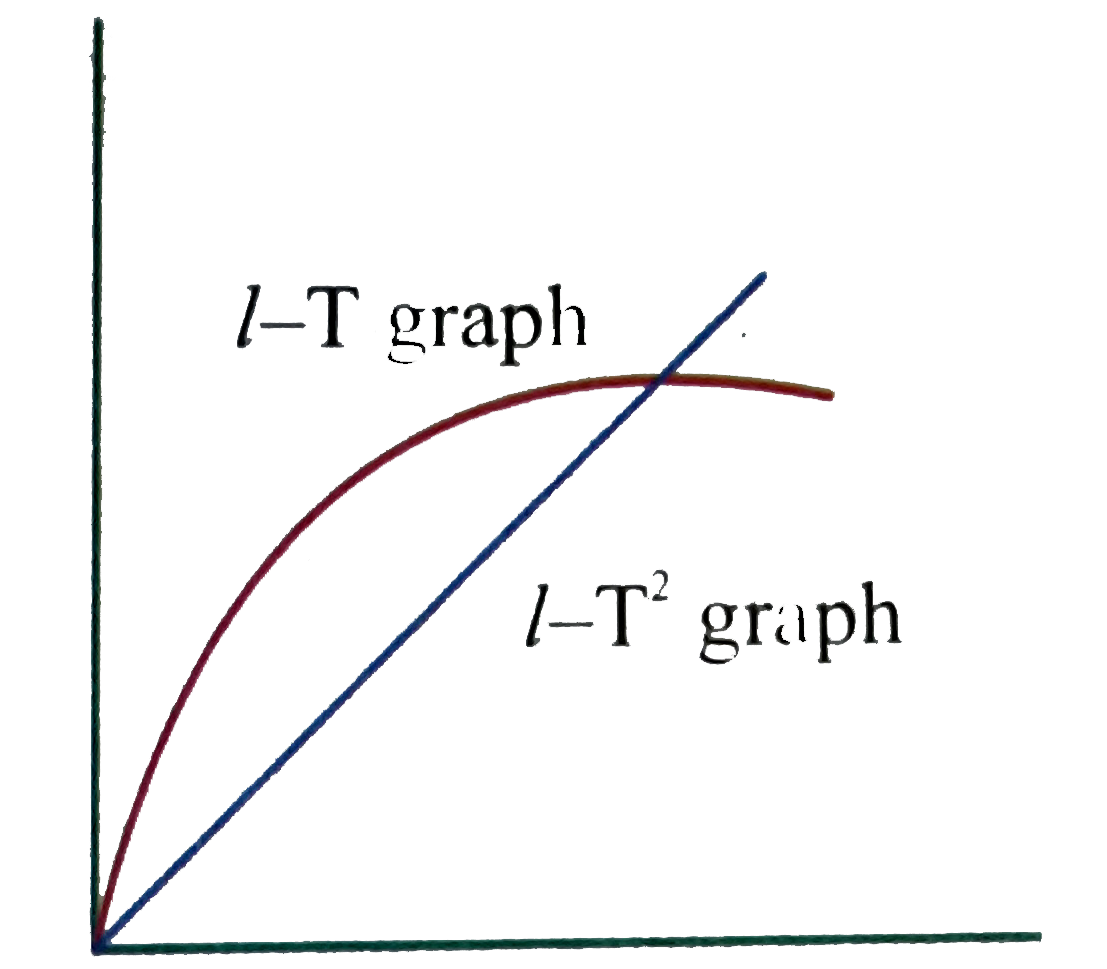
View SolutionA simple pendulum has a time period T. The pendulum is completely immersed in a non-viscous liquid whose density is one-tenth of that of the material of the bob. The time period of the pendulum immersed in liquid is
View SolutionA seconds pendulum is suspended in an elevator moving with constant speed in downward direction. The periodic time (T) of that pendulum is
View SolutionA seconds pendulum is suspended in an elevator moving with constant speed in downward direction. The periodic time (T) of that pendulum is
View Solution
