Find the moment of inertia about the axis shown in the following situations .

Iz=MR22
Using perpendicular axes between
Ix+Iy=Iz
But Ix=Iy from symmetry , ⇒2Iy=Iz=MR22
Iy=MR24

Now The Iy is through CM of the disc , hence Ip=Icm+Md2 (using parallel axes theorem)
Ip=MR24+M(R)2⇒Ip=54MR2

(b) For the rod , Icm=ML212
Ip=Icm+Md2 (using parallel axes theorem )
Ip=ML212+M(L2)2
=ML212+ML24=(1+3)ML212
⇒Ip=ML23

(c) About C1
Iring=MR2
Irod=IC2=IC2+M(R)2
(As C2 is the centre of mass of rod 1 and the distance between the C1 and C2 is d = R)
⇒IRod 1=(ml212+mR2)
Similary , IRod 2=IC2+m(R+l2)2

(As the centre of mass of rod 2 is C3 and it is d = (R+l2) away from C1) .
⇒Irod 2=ml212+m(R+l2)2
Thus Isystem=Iring+Irod 1+Irod 2
=(MR2)+(ml212+mR2)+(ml212+m(R+l2)2)
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - NEET CAFE (TOPICWISE PRACTICE QUESTIONS )
140 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - CHECK YOUR NEET VITALS
14 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
Similar Questions
Knowledge Check
Three rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
 A5mr2B57mr2C7mr2D72mr2
A5mr2B57mr2C7mr2D72mr2
Find the moment of Inertia of a cuboid along the axis as shown in the figure.
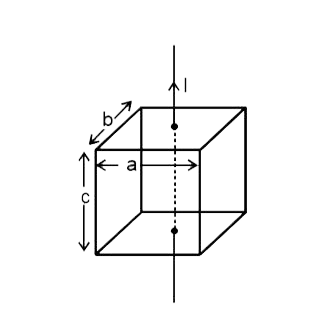
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionThree rings, each of mass m and radius r, are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.

View SolutionFor the structure shown in figure, moment of inertia about an axis passing through yy' is
_PHY_213_Q01.png)
View SolutionFor the structure shown in figure, moment of inertia about an axis passing through yy' is
_PHY_213_Q01.png)
View SolutionFind the moment of inertia of the two uniform joint rods about point P as shown in Fig. Use parallel axis theorem. Mass of each rod is M.
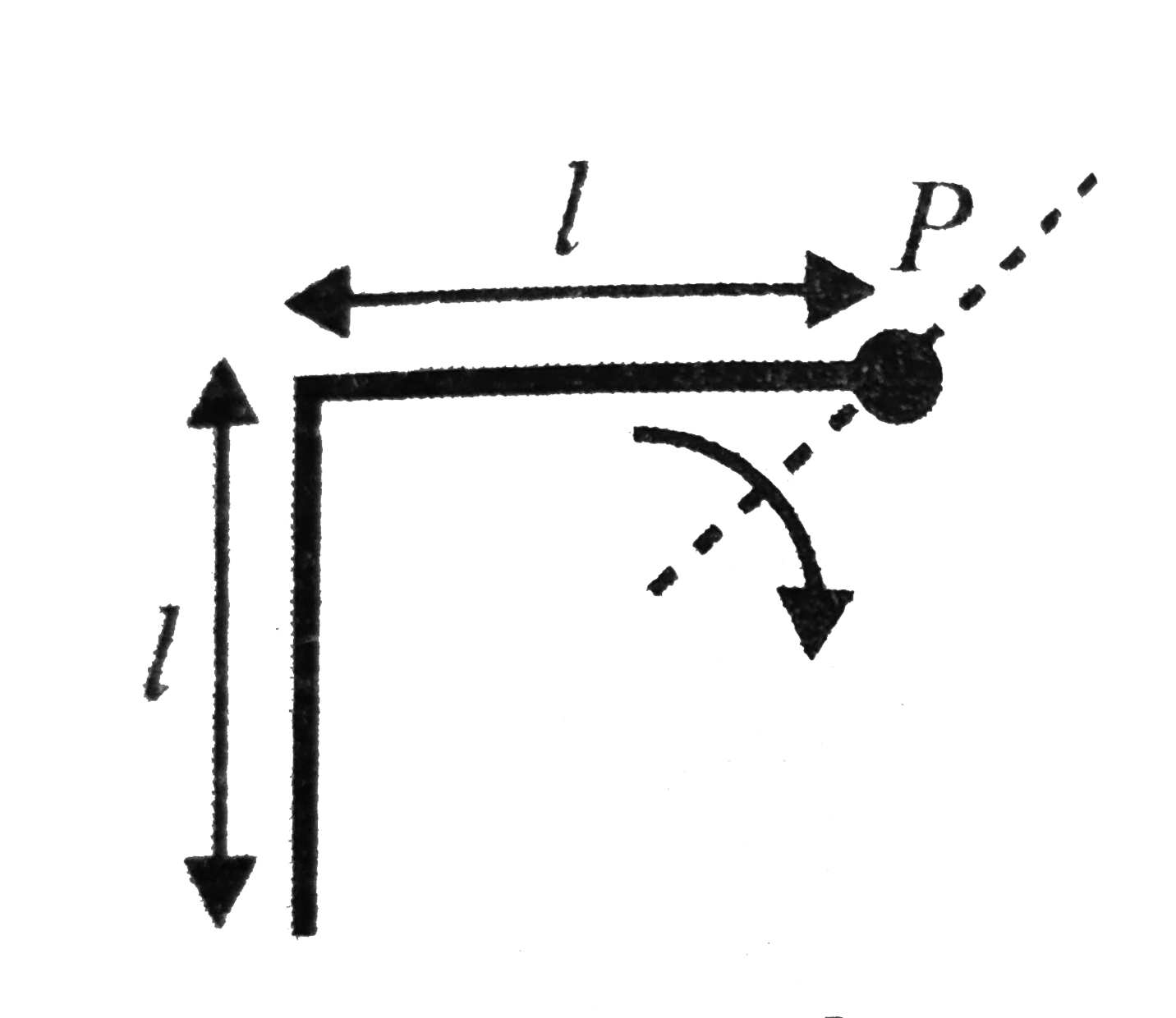
View Solution

