Three point masses, each of mass m, are placed at the corner of an equilateral triangle of side 1. Then the moment of inertia of this system about an axis along one side of the triangle is
3ml2
ml2
34ml2
32ml2
The correct Answer is:C

Moment of inertia about BC is IBC=m(0)2+m(0)2+m(AD)2
Since
AD=√AB2−(BC2)2=√l2−l24=√32l
∴IBC=m(√32l)2=34ml2
Similarly , we find the moment of inertia about AB is IAB=m(0)2+m(0)2+m(CE)2
In right angle ΔBEC
sin60∘=CEBC=CElorCE=lsin60∘=√32l
∴IAB=m(√32l)2=34ml2
Moment of inertia along AC is
IAC=m(0)2+m(0)2+m(BF)2
In right angle ΔBFC
sin60∘=BFBC=BFl or BF=lsin60∘=l√32
∴IAC=m(√32l)2=34ml2
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - CHECK YOUR NEET VITALS
14 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- LAWS OF MOTIONBOOK - MTG GUIDECHAPTER - LAWS OF MOTIONEXERCISE - AIPMT /NEET (MCQ)
24 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
Similar Questions
Three point masses each of mass m are placed at the corners of an equilateral triangle of side 'a' . Then the moment of inertia of this system about an axis passing along one side of the triangle is
View SolutionThree point masses each of mass m are placed at the corners of an equilateral triangle of side 'a'. Then the moment of inertia of this system about an axis passing along one side of the triangle is
View Solution
Knowledge Check
Three point masses, each of mass m, are placed at the corners of an equilateral triangle of side L. The moment of inertia of this system about an axis along one side of the triangle is
AmL2B3mL24C3mL2D3mL22Three point masses each of mass m are placed at the corners of an equilateral triangle of side 'a'. Then the moment of inertia of this system about an axis passing along one side of the triangle is
Ama2B3ma2C34ma2D23ma2Three identical masses, each of mass 1kg, are placed at the corners of an equilateral triangle of side l. Then the moment of inertia of this system about an axis along one side of the triangle is
A3l2Bl2C34l2D32l2
Three point masses each of mass m are placed at the corners of an equilateral triangle of side 'a' . Then the moment of inertia of this system about an axis passing along one side of the triangle is
View SolutionThree point masses, each of mass 2kg are placed at the corners of an equilateral triangle of side 2m. What is moment of inertia of this system about an axis along one side of a triangle?
View SolutionThree point masses each of mass m are placed at the corners of an equilateral triangle of side b. The moment of inertia of the system about an axis coinciding with one side of the triangle is
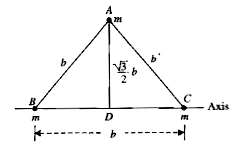
View SolutionThree point masses, each of mass m, are situated at the three corners of an equilateral triangle of each side l. The moment of inertia of this system about one of the sides of the triangle will be -
View SolutionThree point masses m1,m2 and m3 are located at the vertices of an equilateral triangle of side α. What is the moment of inertia of the system about an axis along the altitude of the triangle passing through m1?
View Solution
