यदि y,x का फलन इस प्रकार है कि y(x−y)2=x
कथन-I : ∫dxx−3y=12log[(x−y)2−1] क्योकि
कथन-II : ∫dxx−3y=log(x−3y)+C
कथन-I सत्य है, कथन-II सत्य है, कथन-I का सही स्पष्टीकरण है।
कथन-I सत्य है, कथन-II सत्य है, कथन-II कथन-I का सही स्पष्टीकरण नहीं है।
कथन-I सत्य है परन्तु कथन-II असत्य है।
कथन-I असत्य है परन्तु कथन-II सत्य है।
The correct Answer is:C
Step by step video, text & image solution for यदि y,x का फलन इस प्रकार है कि y(x-y)^(2)=x कथन-I : int(dx)/(x-3y)=(1)/(2)log[(x-y)^(2)-1] क्योकि कथन-II : int(dx)/(x-3y)=log(x-3y)+C by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - INDEFINITE INTEGRATIONEXERCISE - EXERCISE-3 (MISCELLANEOUS TYPE QUESTIONS) (गद्यांश आधारित प्रश्न (गद्यांश #1))2videos
INDEFINITE INTEGRATION
- BOOK - ALLEN HINDICHAPTER - INDEFINITE INTEGRATIONEXERCISE - EXERCISE-3 (MISCELLANEOUS TYPE QUESTIONS) (गद्यांश आधारित प्रश्न (गद्यांश #2))3videos
INDEFINITE INTEGRATION
- BOOK - ALLEN HINDICHAPTER - INDEFINITE INTEGRATIONEXERCISE - EXERCISE-3 (MISCELLANEOUS TYPE QUESTIONS) (स्तम्भ सुमेलन)1videos
INDEFINITE INTEGRATION
- BOOK - ALLEN HINDICHAPTER - ELLIPSEEXERCISE - EXERCISE - 05 - (B)16videos
ELLIPSE
- BOOK - ALLEN HINDICHAPTER - LIMIT EXERCISE - Do yourself29videos
LIMIT
Similar Questions
कई समाकलों की गणना के लिये खण्डश: समाकलन विधि का उत्तरोत्तर उपयोग किया जाता है। खण्डश: समाकलन के लिए निम्न व्यापक सूत्र का उपयोग करने पर परिणाम बहुत जल्दी तथा शुद्ध प्राप्त होता है।
∫u(x)v(x)dx=u(x)v1(x)−u'(x)v2(x)+u''(x)v3(x)−.......+(−1)n−1un−1(x)vn(x)−(−1)n−1∫un(x)vn(x)dx जहाँ v1(x)=∫v(x)dx,v2(x)=∫v1(x)dx......,vn(x)=∫vn−1(x)dx
हम यह मानते है कि इस सूत्र में आने वाले सभी अवकलन तथा समाकलन विद्यमान है। खण्डश: समाकलन के लिए व्यापकसूत्र का उपयोग मुख्यत: तब उपयोगी है जब ∫Pn(x)Q(x)dx, की गणना करना हो जहाँ Pn(x),n कोटि का बहुपद है तथा गुणनखण्ड Q(x) इस प्रकार है कि इसका उत्तरोत्तर समाकलन (n+1) बार हो सकता है।
यदि ∫(x3−2x2+3x−1)cos2xdx=sin2x4u(x)+cos2x8v(x)+C तब-02:10View Solutionफलनों के किसी वर्ग का समाकलन जो एक निश्चित तरिके का अनुकरण करते है, को लघुकरण तथा recursion की विधि द्वारा ज्ञात किया जा सकता है। लघुकरण सूत्रों के उपयोग से किसी समाकलन जो कि घात n>0 पर आश्रित हो जिसे समाकलन कि कोटि कहते है, को छोटी घात के समाकलन में परिवर्तित किया जा सकता है। लघुकरण सूत्रों के निगमन मेंण्डश: समाकलन सहायक होते है। (प्रत्येक प्रश्न में एक अचर जोड़े )
यदि In=∫dx(x2+a2)n हो तो In+1+1−2n2n.1a2In बराबर है-03:55View Solutionनिम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
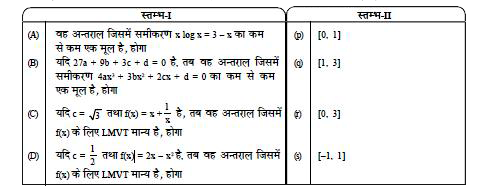 06:47View Solution
06:47View Solutionमाना C1 तथा C2 दो वृत्त हैं, C2,C1 के अन्दर स्थित है। एक वृत्त, C,C1 के अन्दर स्थित है तथा C1 को अन्तः तथा C2 को बाह्य स्पर्श करता है। C के केन्द्र का बिन्दुपथ ज्ञात कीजिए।
02:43View Solutionफलन y = f (x) के आरेख के सापेक्ष निम्न में से कौन से कथन सत्य या असत्य होंगे :
limn→−1+f(x)=1
 05:44View Solution
05:44View SolutionIf log (x2+y2)=tan−1 (yx), then show that dydx=x+yx−y
01:45View SolutionThe solution of the differential equation dydx=x+yx satisfying the condition y(1)=1 is (1) y=lnx+x (2) y=xlnx+x2 (3) y=xe(x−1) (4) y=xlnx+x
08:57View SolutionIf y=ax^ax^(.).ˆ((((∞)))),provethatdydx=y2logyx(1−ylogx.logy)
02:54View SolutionIf log(x2+y2)=2tan−1(yx), show that dydx=x+yx−y .
06:32View SolutionIf y(x-y)^(2)=x, then int(1)/(x-3y)dx is equal to (A) (1)/(3)log{(x-y)^(2)+1}(B)(1)/(4)log{(x-y)^(2)-1}(C)(1)/(2)log{(x-y)^(2)-1}(D)(1)/(6)log{(x^(2)-y^(2)-1}
08:41View SolutionThe solution of the differential equation dydx=x2+xy+y2x2, is a. tan−1(xy)=logy+C b. tan−1(yx)=logx+C c. tan−1(xy)=logx+C d. tan−1(yx)=logy+C
07:54View SolutionThe solution of dydx+xy2−x2y3x2y+2x3y2=0, is (A) log(y2x)−1xy=C (B) log(xy)+y2x=C (C) log(x2y)+y2x=C (D) none of these
07:45View SolutionIf log(x2+y2)=2tan−1(yx), show that dydx=x+yx−y
04:27View SolutionStatement I If y is a function of x such that y(x−y)2=x, then ∫dxx−3y=12[log(x−y)2−1]
Statement II ∫dxx−3y=log(x−3y)+C02:42View SolutionIf y is implicit differentiable function of x such that y(x+y)2=x then ∫dxx+3y
04:16View Solution

