अनुक्रम S=i+2i2+3i3+…….100 पदों तक, जहां i=√−1 है, होगा:
50(1−i)
25i
25(1+i)
100(1−i)
The correct Answer is:A
Step by step video, text & image solution for अनुक्रम S=i+2i^(2)+3i^(3)+…….100 पदों तक, जहां i=sqrt(-1) है, होगा: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE -02 (सही विकल्प चुनिए)10videos
COMPLEX NUMBER
- BOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE -3 MISCELLANEOUS TYPE QUESTIONS9videos
COMPLEX NUMBER
- BOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - DO YOURSELF 92videos
COMPLEX NUMBER
- BOOK - ALLEN HINDICHAPTER - AREA UNDER THE CURVEEXERCISE - Exercise-05 [B]21videos
AREA UNDER THE CURVE
- BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -05 [B] (JEE-ADVANCED: PREVIOUS YEAR QUESTIONS)2videos
CONTINUITY
Similar Questions
आर्गण्ड समतल पर माना α=−2+3z,β=2−3z तथा |z|=1 है तो सत्य कथन है
02:31View Solutionनिम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
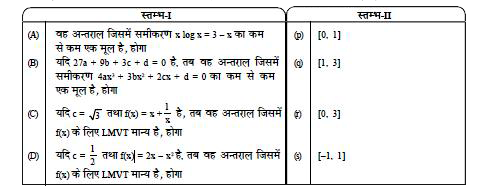 05:09View Solution
05:09View Solutionयदि ω इकाई का काल्पनिक घनमूल हो तो (1+ω−ω2)2 बराबर होगा
View Solutionवक्र f(x)=x2+bx−b के बिन्दु (1,1) पर स्पर्श रेखा तथा निर्देशी अक्षो से बना त्रिभुज प्रथम चतुर्थांश में स्थित है | यदि इसका क्षेत्रफल 2 है, तो b का मान है -
03:37View Solutionफलन f(x)=⎧⎨⎩e1/x−1e1/x+1जबx≠01जबx=0 का x=0 पर सततता का परीक्षण कीजिए।
03:42View SolutionFind the conjugate of (3−2i)(2+3i)(1+2i)(2−i).
05:11View SolutionThe sequences S=i+2i^(2)+3i^(3)+...... upto 100 terms simplifies to where i=sqrt(-1)
03:32View SolutionExpress each of the following in the form (a + ib) :
(i)1(4+3i)(ii)(3+4i)(4−5i)(iii)(5+√2i)(1−√2i)(iv)(−2+5i)(3−6i)(v)(3−4i)(4−2i)(1+i)(vi)(2−2i)(2+3i)(1+2i)(2−i)(vii)(2+3i)(2−i)(viii)(1−i)3(1−i3)(ix)(1+2i)3(1+i)(2−i)07:48View SolutionShow that
(i) {(3+2i)(2−3i)+(3−2i)(2+3i)} is purely real,
(ii) ⎧⎪ ⎪⎨⎪ ⎪⎩(√7+i√3)(√7−i√3)+(√7−i√3)(√7+i√3)⎫⎪ ⎪⎬⎪ ⎪⎭ is purely real.View Solution(3−2i)(2+3i)(1+2i)(2−i) का संयुग्मी ज्ञात कीजिए ।
03:00View SolutionIf z=∣∣ ∣∣3+2i5−i7−3ii2i−3i3−2i5+i7+3i∣∣ ∣∣,where i=√−1,then
03:50View Solution(3−2i)(2+3i)(1+2i)(2−i) का संयुग्मी ज्ञात कीजिए।
04:40View SolutionFind the conjuate of (3−2i)(2+3i)(1+2i)(2−i).
06:04View Solutiona + ib के रूप में प्रकट कीजिए :
(i)5−3i6+i(ii)4−2i2+3i(iii)2+3i−5−4i(iv)2−√−251−√−16(v)2i2+6i3+3i16−6i19+4i25(vi)(√5−7i)2+(−2+7i)2(vii)13+4i(viii)(1+i1−i)3(ix)(2+i)33+2i(x)1+2i+3i21−2i+3i2(xi)√3+i√22√3+i√2(xii)(1+i)3(2+i)(1+2i)09:48View SolutionFind the conjugate of (3−2i)(2+3i)(1−2i)(2−i)
04:20View Solution

