सम्मिश्र संख्याओं z तथा ω के लिए सिद्ध कीजिए कि |z|2ω−|ω|2z=z−ω होगा यदि z=ω या z¯¯ω=1 हो।
Step by step video & image solution for सम्मिश्र संख्याओं z तथा omega के लिए सिद्ध कीजिए कि |z|^(2) omega-|omega|^(2)z=z-omega होगा यदि z=omega या z bar(omega)=1 हो। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPLEX NUMBERBOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE 4 (B) Brain storming subjective exercise
9 Videos
- COMPLEX NUMBERBOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE -5 (A) JEE (MAIN) : PREVIOUS YEAR QUESTIONS
18 Videos
- COMPLEX NUMBERBOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE -3 MISCELLANEOUS TYPE QUESTIONS
9 Videos
- AREA UNDER THE CURVEBOOK - ALLEN HINDICHAPTER - AREA UNDER THE CURVEEXERCISE - Exercise-05 [B]
21 Videos
- CONTINUITY BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -05 [B] (JEE-ADVANCED: PREVIOUS YEAR QUESTIONS)
2 Videos
Similar Questions
सभी वास्तविक संख्याओं x के लिये, माना प्रतिचित्रण f(x)=1x−i, जहाँ i=√−1 है। यदि वास्तविक संख्याएँ a, b, c तथा d जिनके लिये f (a), f (b), f (c) तथा f (d) सम्मिश्र तल में एक वर्ग का निर्माण करते है। वर्ग का क्षेत्रफल ज्ञात कीजिये।
View Solutionअसमिका |z−4|<|z−2| किस क्षेत्र को निरूपित करती है
View Solutionनिम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
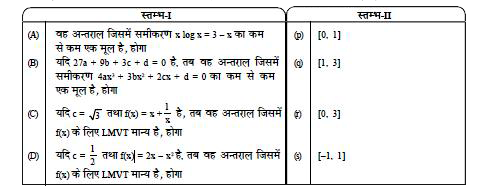
View Solutionवक्र f(x)=x2+bx−b के बिन्दु (1,1) पर स्पर्श रेखा तथा निर्देशी अक्षो से बना त्रिभुज प्रथम चतुर्थांश में स्थित है | यदि इसका क्षेत्रफल 2 है, तो b का मान है -
View Solutionफलन f(x)=⎧⎨⎩e1/x−1e1/x+1जबx≠01जबx=0 का x=0 पर सततता का परीक्षण कीजिए।
View SolutionLet z and w be two complex numbers such that |Z|<=1,|w|<=1 and |z+iw|=|z-ibar(w)|=2
View SolutionLet z and w are two non zero complex number such that |z|=|w|, and Arg(z)+Arg(w)=pi then (a) z=w( b) z=bar(w)(c)bar(z)=bar(w)(d)bar(z)=-bar(w)
View SolutionFor complex numbers z and w, prove that |z|^(2)w-|w|^(2)z=z-w, if and only if z=w or zbar(w)=1.
View SolutionLet z and omega be two complex numbers such that |z|<=1,| omega|<=1 and |z+omega|=|z-1vec omega|=2 Use the result |z|^(2)=zz and |z+omega|<=|z|+| omega|
View SolutionIf omega is any complex number such that z omega = |z|^2 and |z - barz| + |omega + bar(omega)| = 4 then as omega varies, then the area bounded by the locus of z is
View SolutionIf |z|≤1and|ω|≤1, show that |z−ω|2≤(|z|−|ω|)2+(argz−argω)2
View Solutionयदि |z|≤1,|w|≤1, तो दिखाइए कि |z−w|2≤(|z|−|w|)2+{कोणांक(z)−कोणांक(w)}^(2)
View Solutionसम्मिश्र संख्याओं z तथा ω के लिए सिद्ध कीजिए कि |z|2ω−|ω|2z=z−ω होगा यदि z=ω या z¯¯ω=1 हो।
View SolutionIf z and omega are two non-zero complex numbers such that |z omega|=1" and "arg(z)-arg(omega)=(pi)/(2) , then bar(z)omega is equal to
View SolutionFor complex numbers zandw, prove that |z|2w−|w|2z=z−w, if and only if z=w or z¯¯¯w=1.
View Solution
