यदि x = a पर 'f' संतत् तथा 'g' असंतत् है, तब f(x).g(x),x=a पर असंतत् है|
The correct Answer is:f
Step by step video, text & image solution for यदि x = a पर 'f' संतत् तथा 'g' असंतत् है, तब f(x).g(x), x=a पर असंतत् है| by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) (स्तम्भ सुमेलन (Match the column))
1 Videos
- CONTINUITY BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) (कथन एवं कारण (Assertion & Reason))
6 Videos
- CONTINUITY BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -02 (BRAIN TEASERS) ( सही विकल्पों को चुनिए (एक या एक से अधिक सही उत्तर हैं)
14 Videos
- COMPLEX NUMBERBOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE 5 (B) JEE (ADVANCED) : PREVIOUS YEAR QUESTIONS
36 Videos
- DEFINITE INTEGRATIONBOOK - ALLEN HINDICHAPTER - DEFINITE INTEGRATIONEXERCISE - Exercise - 05 B
38 Videos
Similar Questions
निम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
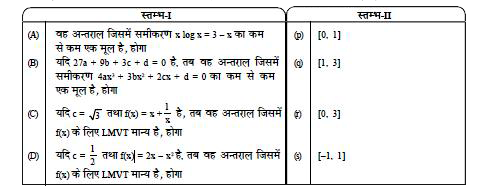
View Solutionकथन-I : f(x)=sinx+[x],x=0 असंतत् है। क्योंकि
कथन-II: यदि x=a पर g(x) संतत् तथा h(x) असंतत् है, तब g(x)+h(x),x=a पर आवश्यक रूप से असंतत् होगा।
View Solutionमाना खण्डित परिभाषित फलन f(x)=⎧⎪⎨⎪⎩√−x यदिx<00 यदि0≤x≤4x−4 यदिx>4 है। सही विकल्प चुने जो फलन की संतत्ता को परिभाषित करता हो-
View Solutionयदि z1,z2,z3 सम्मिश्र संख्याएँ इस प्रकार है कि |z1|=|z2|=|z3|=∣∣∣1z1+1z2+1z3∣∣∣=1, तब |z1+z2+z3| है:
View Solutionसिद्ध कीजिए कि ∫e2e−1∣∣∣logexx∣∣∣dx=52
View Solutionयदि f'(a) विधमान है तब limx→axf(a)−af(x)x−a=
View Solutionf(x)={sin1xx≠01x=0 पर संतत है अथवा असंतत ।
View Solutionमाना कि f:Z→Z इस प्रकार परिभाषित है:
f(x)={x, यदि x सम हैx+1, यदि x विषम है
क्या g:Z→Z का अस्तित्व है ताकि
View Solutionसिद्ध कीजिए की फलन f(x)=5x-3,x=0 पर सतत है।
View Solutionमान लीजिए कि f:[0,1]→[0,1],f(x)={x,यदि x परिमेय है1−x,यदि x अपरिमेय है द्वारा परिभाषित है , तो (fof)x:
View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
View Solutionयदि द्विअवकलनीय f(x) फलन x=a पर स्थानीय उच्चिष्ठ है , तो
View Solutionयदि f(x)=x2−3x तो वे बिंदु जिन पर f(x)=f'(x) है ,होंगे -
View Solutionयदि dydx=ex+y और दिया है x=1 पर y=1, तब x=−1 पर y ज्ञात कीजिए |
View Solutionयदि f(x)=2−xcosx2+xcosx तथा g(x)logex,(x>0) है, तो समाकल π/4∫−π/4g(f(x))dx का मान है
View Solutionयदि 3x=4x−1 तब x बराबर है
View Solution
