माना f(x)=⎧⎪
⎪⎨⎪
⎪⎩2sin(acos−1x)यदिx∈(0,1)√3यदिx=0ax+bयदिx<0 कथन-I : यदि b=√3 तथा a=23 तो f(x),(−∞,1) में संतत् होगा। क्योंकि
कथन-II : यदि फलन अन्तराल 1 में परिभाषित है तथा अन्तराला के प्रत्येक बिन्दु पर सीमा विद्यमान है, तो फलना में संतत् होगा।
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है।
कथन-I सत्य है,कथन-II सत्य है: कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
कथन - I सत्य है परन्तु कथन - II असत्य है।
कथन - I असत्य है परन्तु कथन - II सत्य है।
The correct Answer is:C
Step by step video, text & image solution for माना f (x) = {{:(2sin (acos^(-1)x),"यदि" x in (0,1)),(sqrt(3),"यदि" x=0),(ax+b,"यदि" x lt 0):} कथन-I : यदि b=sqrt(3) तथा a=2/3 तो f (x),(-infty,1) में संतत् होगा। क्योंकि कथन-II : यदि फलन अन्तराल 1 में परिभाषित है तथा अन्तराला के प्रत्येक बिन्दु पर सीमा विद्यमान है, तो फलना में संतत् होगा। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONTINUITY BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) (गद्यांश आधारित प्रश्न (Comprehension Based Questions)) गद्यांश # 1
3 Videos
- CONTINUITY BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -04 [A] CONCEPTUAL SUBJECTIVE EXERCISE)
10 Videos
- CONTINUITY BOOK - ALLEN HINDICHAPTER - CONTINUITY EXERCISE - EXERCISE -03 (MISCELLANEOUS TYPE QUESTIONS) (स्तम्भ सुमेलन (Match the column))
1 Videos
- COMPLEX NUMBERBOOK - ALLEN HINDICHAPTER - COMPLEX NUMBEREXERCISE - EXERCISE 5 (B) JEE (ADVANCED) : PREVIOUS YEAR QUESTIONS
36 Videos
- DEFINITE INTEGRATIONBOOK - ALLEN HINDICHAPTER - DEFINITE INTEGRATIONEXERCISE - Exercise - 05 B
38 Videos
Similar Questions
यदि Sn(x)=xx+1+x2(x+1)(x2+1)+....+x2n(x+1)(x2+1)...(x2n+1) तथा x>1,limn→∞Sn(x)=l
g(x)={√ax+b−1xx≠01x=0
h:R→R,h(x)=x9−6x8−2x7+12x6+x4−7x3+6x2+x−7
यदि g(x),x=0 पर संतत् है, तो a+b बराबर है-
View Solutionयदि f(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩−x2जबx≤05x−4जबx<x≤14x2−3xजब1<x<23x+4जबx≥2 f(x) की R में संतता की जांच कीजिए|
View Solutionनिम्न प्रश्न में दो स्तम्भ में वक्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है।स्तम्भ-I (Column-I) के वक्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्तव्यस्तम्भ-II (Column-II) के एक या एक से अधिक वक्तव्य (वक्तव्यों) से सही सुमेल करता है।
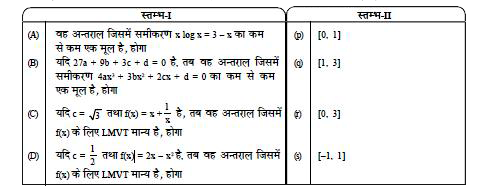View Solutionयदि z1,z2,z3 सम्मिश्र संख्याएँ इस प्रकार है कि |z1|=|z2|=|z3|=∣∣∣1z1+1z2+1z3∣∣∣=1, तब |z1+z2+z3| है:
View Solutionसिद्ध कीजिए कि ∫e2e−1∣∣∣logexx∣∣∣dx=52
View Solutionफलन f(x) की x = 0,1 पर सांतत्य का परिक्षण कीजिए जब
f(x)=1−2x यदि x<01 यदि 0≤x<12x−1 यदि x≥1
View Solutionयदि प्रदत फलन बिन्दु x = 0 पर संतत हो, तो a, b व c के मान ज्ञात कीजिए -
f(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩sin(a+1)x+sinxx,यदिx<0 c,यदिx=0√x+bx2−√xbx3/2,यदिx>0
View Solutionf(x)=⎧⎪⎨⎪⎩ 2,यदिx≤3ax+b,यदि3<x<5 9,यदिx≥5
View Solutionf(x)=⎧⎪⎨⎪⎩ 4,यदिx≤−1ax2+b,यदि−1<x<0cosx,यदिx≥0
View Solutionयदि f(x)=ax+bx+1,limx→0f(x)=2 तथा limx→∞f(x)=1, तो सिद्ध कीजिए f(−2)=0
View Solutionमान लीजिए कि f:[0,1]→[0,1],f(x)={x,यदि x परिमेय है1−x,यदि x अपरिमेय है द्वारा परिभाषित है , तो (fof)x:
View Solutionयदि द्विअवकलनीय f(x) फलन x=a पर स्थानीय उच्चिष्ठ है , तो
View Solutionनिम्न कथन सत्य या असत्य है
यदि f(x)=√x−2 तो : fof=f2
View Solutionयदि f(x)=xयदिx परिमेय है 0यदिx अपरिमेय है तथा g(x)=0यदिx परिमेय हैx यदिx अपरिमेय है तबf−g है
View Solutionयदि फलन f(x)={xsin(1x)x≠0ax=0
x=0, पर सतत् है, तो a का मान है
View Solution