f(x)=sin(πxn−1)+cos(πxn)netcZ,n<2 का आवर्तनांक है।
2π(n−1)
4n(n−1)
2n(n−1)
इनमें से कोई नही
The correct Answer is:C
Step by step video, text & image solution for f(x) = sin ((pi x)/(n-1)) + cos ((pi x)/(n )) n etc Z , n lt 2 का आवर्तनांक है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - Solved Multiple Choice Question (त्रिभुज की भुजाओ तथा कोणों के माध्य सम्बन्ध त्रिभुजो के हल )82videos
त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी
- BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - Solved Multiple Choice Question (त्रिभुजों से सम्बध्द वृत्त )10videos
त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी
- BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - Solved Multiple Choice Question (त्रिकोणमितीय समीकरण के हल)58videos
त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी
- BOOK - ERRORLESS HINDICHAPTER - गणितीय तर्कशास्त्रEXERCISE - Jee Advanced (Reasoning )3videos
गणितीय तर्कशास्त्र
- BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)5videos
त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकाये
Similar Questions
यदि त्रिभुज ABC में a=5,b=7 व sinA=34 है। तब इस प्रकार के कितने त्रिभुज सम्भ्व है।
01:26View Solutionएक त्रिभुज में यदि r1=2r2=3r3 तब ab+bc+ca बराबर है।
02:44View Solutionयदि sin2θ−cosθ−14=0 तो θ का व्यापक मान हैं
01:56View Solutionकथन - 1 : ~ (p ↔ ~ q) और p ↔ q तुल्यमान (equivalent) हैं।
कथन -2: ~ (p↔ ~q) एक पुनरुक्ति (tautology) है ।05:51View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
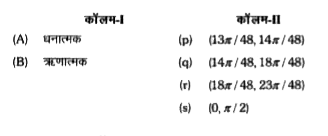 03:11View Solution
03:11View SolutionThe function f(x)=tanx is discontinuous on the set (a){nπ;n∈Z} (b) {2nπn∈Z} {(2n+1)π2:n∈Z} (d) {nπ2:n∈Z}
10:02View SolutionThe period of the function f(x)=cos(pi(x)/(n!))-sin(pi(x)/((n+1)!)) is
01:59View SolutionThe general solution of the equation sinx−3sin2x+sin3x=cosx−3cos2x+cos3x is (n∈Z) nπ+π8 (b) nπ2+π8 (−1)nnπ2+π8 (d) 2nπ+cos−123
02:22View SolutionLet tanx−tan2x>0 and |2s∈x|<1 . Then the intersection of which of the following two sets satisfies both the inequalities? x>nπ,n∈Z (b) x>nπ−π6,n∈Z x<nπ−π4,n∈Z (d) x<nπ+π6,n∈Z
06:42View SolutionFind the period of f(x)=sin(πx)n!−cos(πx)(n+1)!
03:04View SolutionIf A(x)=det[[x^(n),sin x,cos xn!sin((n pi)/(2)),cos((n pi)/(2))a,a^(2),a^(3)]], then the value of (d^(n))/(dx^(n))[Delta(x)] at x=0 is
04:36View SolutionThe domain of f (x) = sqrt (log ((1)/(| sin x |))) is (i) (-oo, oo) (ii) R-{(n pi)/(2): n in Z} (iii) R-{(n pi): n in Z} (iv) R-{(n pi)+(-1)^(n) ((pi)/(2)): n in Z }
03:31View SolutionThe period of f(x)=sin((pi x)/(n-1))+cos((pi x)/(n)),n in Z,n>2
04:28View SolutionProve that
(i) cos (n + 2) x cos (n+1) x +sin (n+2) x sin (n+1) x = cos x)
(ii) cos .(π4−x) cos .(π4−y) - sin (π4−x) sin (π4−y)= sin (x+y)01:01View SolutionIf 0<x<π2 and sinnx+cosnx≥1, then
04:24View Solution

