समीकरण cos2x−2cosx=4sinx−sin2x(0<x<π) का व्यापक हल होगा।
π−cot−1(12)
πtan−1(2)
π+tan−1(12)
इनमें से कोई नही
The correct Answer is:B
Step by step video, text & image solution for समीकरण cos^(2) x-2 cos x=4 sin x- sin 2x (0 lt x lt pi) का व्यापक हल होगा। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - JEE Advanced
47 Videos
- त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - Solved Multiple Choice Question (ऊँचाई एवं दूरी)
35 Videos
- गणितीय तर्कशास्त्रBOOK - ERRORLESS HINDICHAPTER - गणितीय तर्कशास्त्रEXERCISE - Jee Advanced (Reasoning )
3 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
Similar Questions
0<θ<π2 के लिए 6Σm=1cosec(θ+(m−1)π4)cosec(θ+mπ4)=4√2 का के हल निम्न है।
View Solutionभूमि के एक बिन्दु पर एक मीनार के शिखर का उन्त्रयन कोण 30∘ है यदि मीनार की और 20 मीटर चलने पर उन्यन कोण 60∘ हो जाता है तो मीनार की ऊँचाई हैं
View Solutionकथन - 1 : ~ (p ↔ ~ q) और p ↔ q तुल्यमान (equivalent) हैं।
कथन -2: ~ (p↔ ~q) एक पुनरुक्ति (tautology) है ।
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
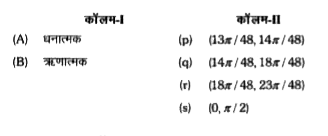
View Solution...sin8x≤sin6x≤sin4x≤sin2x≤1 also ....cos8x≤cos6x≤cos4x≤cos2x≤1
View SolutionNumber of solutions of the equation cos42x+2sin22x
=17(cosx+sinx)8,0<x<2π is
View Solutionनिम्नलिखित का अवकल गुणांक ज्ञात कीजिए ।
(sinx−cosx)sinx−cosx,π4<x<3π4
View Solutioncos−1(sinx+cosx√2),π4<x<5π4
View SolutionIf f(x)=⎧⎨⎩sin2x√1−cos2x, for 0<x<π2cosxπ−2x, for π2<x<π, then
View SolutionIf cosx+sinx=a(−π2<x<−π4), then cos2x is equal to
View SolutionIf sin22x+4sin4x−4sin2x⋅cos2x4−sin22x−4sin2x=19 and 0<x<π. Then the value of x is :
View SolutionWrite the simplest from of tan−1(cosx−sinxcosx+sinx),0<x<π2
View Solutionइन को सरलतम रूप में लिखिए tan−1cosx−sinxcosx+sinx−π4<x<π4
View Solutionफलन tan−1(cosx−sinxcosx+sinx),0<x<2π को सरलतम रूप में लिखिए ।
View SolutionDifferentiate cos−1(sinx+cosx√2),−π4<x<π4
View SolutionFor 0<x<π2, prove that cos(sinx)>sin(cosx).
View Solution
