असमिका 2sinθ+2cosθ≥21−1√2θ के सभी वास्तविक मानो के लिए सत्य है।
कथन -1 सही है कथन -2 सही है कथन -1 के लिए कथन -2 का स्पष्टीकरण सही है।
कथन -1 सही है कथन -2 सही है कथन -1 के लिए कथन -2 का स्पष्टीकरण सही नही है।
कथन -1 सही है। कथन -2 गलत है।
कथन-1 गलत है। कथन -2 सही है।
Step by step video & image solution for असमिका 2 ^(sin theta) + 2 ^(cos theta) ge 2^(1-(1)/(sqrt(2))) theta के सभी वास्तविक मानो के लिए सत्य है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी BOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय समीकरण एवं असमिकाएँ त्रिभुजों के गुण उँचाई एवं दुरी EXERCISE - Exercise
134 Videos
- गणितीय तर्कशास्त्रBOOK - ERRORLESS HINDICHAPTER - गणितीय तर्कशास्त्रEXERCISE - Jee Advanced (Reasoning )
3 Videos
- त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेBOOK - ERRORLESS HINDICHAPTER - त्रिकोणमितीय अनुपात, फलन एवं सर्वसमिकायेEXERCISE - JEE Advanced (Matrix Match type questions)
5 Videos
Similar Questions
यदिsin2θ=cosθ,0<θ<π तो θ के संभव मान है।
View Solutionकथन - 1 : ~ (p ↔ ~ q) और p ↔ q तुल्यमान (equivalent) हैं।
कथन -2: ~ (p↔ ~q) एक पुनरुक्ति (tautology) है ।
View Solutionनिम्नलिखित कॉलम I को कॉलम II से मिलाये
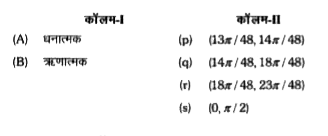
View SolutionProve the following identity: (1sec2θ−cos2θ+1cosec2θ−sin2θ)sin2θcos2θ=1−sin2θcos2θ2+sin2θcos2θ
View Solution(cos^(2)theta(1-cos theta))/(sin^(2)theta(1-sin theta))=(1+sin theta)/(1+cos theta)
View SolutionIf (sinθ+cosθ)=√2cosθ, show that cotθ=(√2+1).
View Solutionसिद्ध कीजिए : (1sec2θ−cos2θ+1 cosec 2θ−sin2θ).sin2θcos2θ=1−sin2θcos2θ2+sin2θcos2θ
View Solutionsin2θ1−cosθ−cos2θ1−sinθ=cosθ−sinθ
View SolutionIf ∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣=0, then the value of θ is
View SolutionIf (sinθ+cosθ)=√2cosθ, show that cotθ=(√2+1).
View SolutionIf ∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣=0, then the value of θ is
View Solutionsin22θ+cos42θ=34 को संतुष्ट करने वाले θ∈(0,π2) के सभी मानो का योग है
View Solution3cosθ+5sin(θ−π6) का θ के किसी भी वास्तविक मान के लिए अधिकतम मान है
View Solutionअसमिका 2sinθ+2cosθ≥21−1√2θ के सभी वास्तविक मानो के लिए सत्य है।
View Solutionयदि ∣∣ ∣ ∣∣1+sin2θcos2θ4sin4θsin2θ1+cos2θ4sin4θsin2θcos2θ1+4sin4θ∣∣ ∣ ∣∣ =0 तब θ का मान होगा
View Solutionनिम्नलिखित सर्व समिकाओ को सिद्ध करो-
(i) (1−cosθ)(1+cosθ)(1+cot2θ)=1
(ii) (1+sinθ)2+(1−sinθ)2)2cos2θ=1+sinθ21−sin2θ
(iii) cos2θ(1−cosθ)sin2θ(1−sinθ)=1+sinθ1+cosθ
(iv) (sinθ−cosθ)2=1−2sinθ.cosθ
(v) (sinθ+cosθ)2+(sinθ−cosθ)2=2
(vi) (asinθ+bcosθ)2+(acosθ−bsinθ)2=a2+b2
(vii) cos4A+sin4A+2sin2A.cos2A=1
(ix) (cos4θ−sin4θ)=cos2θ−sin2θ=2cos2θ−1
(x) 2cos2θ−cos4θ+sin4θ=1
(xi) 1−2cos2θ+cos4θ=sin4θ
(xii) 1−2sin2θ+sin4θ=cos4θ
View Solution
