The work-energy theorem states that the change in
kinetic energy of a particle is equal to the work done on it by the net force
kinetic energy of a particle is equal to the work done by one of the forces acting on it
potential energy of a particle is equal to the work done on it by the net force
potential energy of a particle is equal to the work done by one of the forces acting on it
The correct Answer is:A
To solve the question regarding the work-energy theorem, we need to define what the theorem states. Here's a step-by-step breakdown:
Step 1: Understand the Work-Energy Theorem
The work-energy theorem is a fundamental principle in physics that relates the work done on an object to its kinetic energy.
Step 2: Define the Work-Energy Theorem
The theorem states that the change in kinetic energy of an object is equal to the net work done on it by the forces acting on it.
Step 3: Write the Mathematical Expression
Mathematically, the work-energy theorem can be expressed as:
W=ΔKE
where:
- W is the work done on the object,
- ΔKE is the change in kinetic energy, defined as KEfinal−KEinitial.
Step 4: Identify the Correct Option
Given the options, the correct statement according to the work-energy theorem is that the change in kinetic energy is equal to the work done on the body by the net force acting on it.
Conclusion
Thus, the answer to the question is that the work-energy theorem states that the change in kinetic energy is equal to the work done on a body.
---
The work-energy theorem is a fundamental principle in physics that relates the work done on an object to its kinetic energy.
The theorem states that the change in kinetic energy of an object is equal to the net work done on it by the forces acting on it.
Mathematically, the work-energy theorem can be expressed as:
W=ΔKE
where:
- W is the work done on the object,
- ΔKE is the change in kinetic energy, defined as KEfinal−KEinitial.
Given the options, the correct statement according to the work-energy theorem is that the change in kinetic energy is equal to the work done on the body by the net force acting on it.
Thus, the answer to the question is that the work-energy theorem states that the change in kinetic energy is equal to the work done on a body.
Topper's Solved these Questions
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT
18 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - ASSERTION & REASON
15 Videos
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
An ideal gas undergoing a change of state from A to B through four different paths I, II,III and IV as shown in the P-V diagram that lead to the same change of state tyhen the change in internal energy is
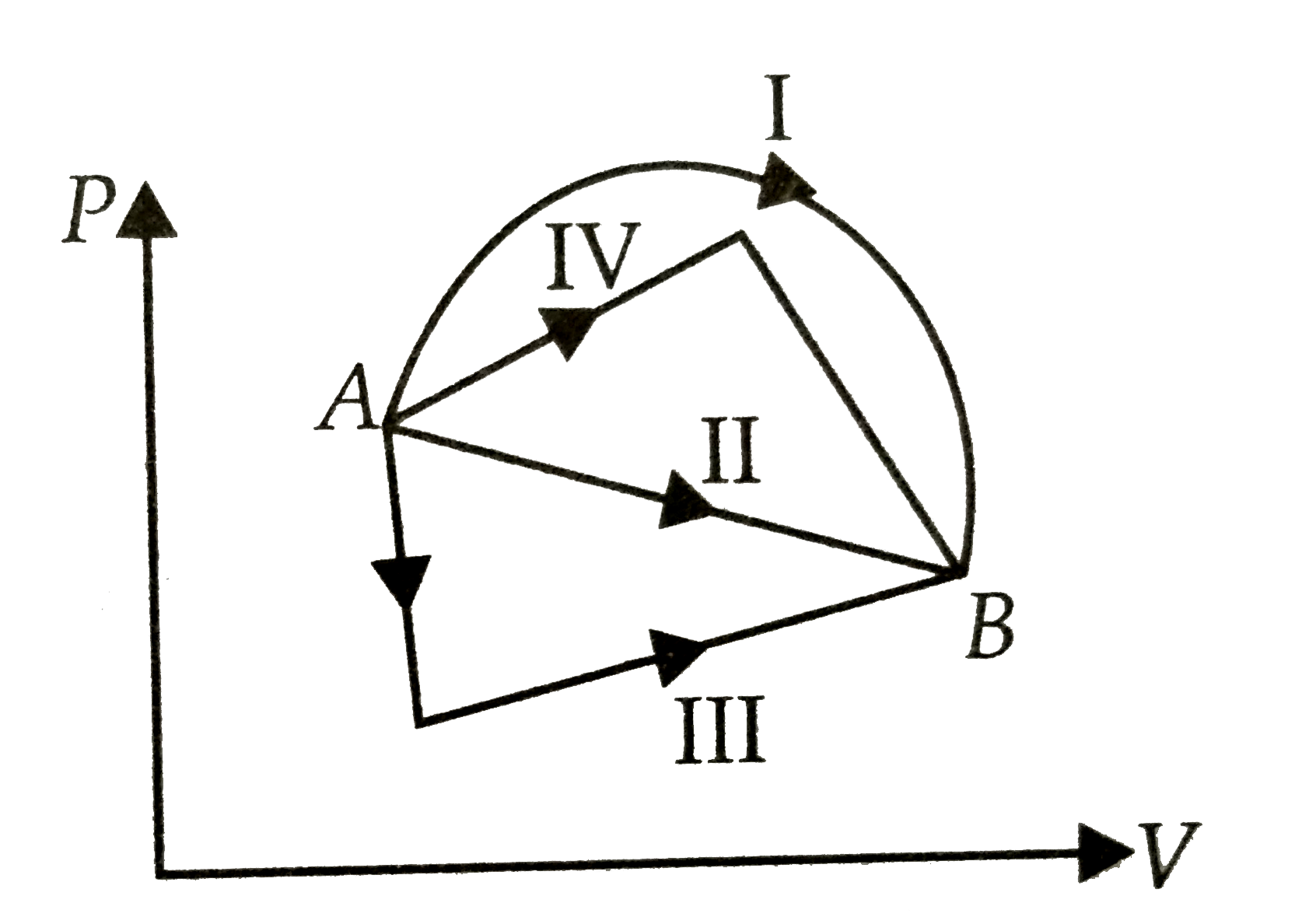 Asame in I and II but not in III and IVBsame in III and IV but not I I and IICsame in I, II and III but not I IVDsame in all the four cases
Asame in I and II but not in III and IVBsame in III and IV but not I I and IICsame in I, II and III but not I IVDsame in all the four cases
In a process, 701 J of heat is absorbed by a system and 394 J of work is done by the system. What is the change in internal energy of the process?
View SolutionIn a process, 701J of heat is absorbed by a system and 394J of work is done by the system. What is the change in internal energy for the process?
View SolutionIf 150 J of heat is added to a system and the work done by the system is 110 j. then change in internal energy wil be
View SolutionFor a gaseous system, if heat rejected by the system is 100J and work done by the system is 20J , then change in internal energy is
View SolutionWork energy theorem is applicable
View SolutionThe total work done on a particle is equal to the change in its kinetic energy
View SolutionShow that the work done to rotate a body is equal to the change in rotational kinetic energy,
View Solution
