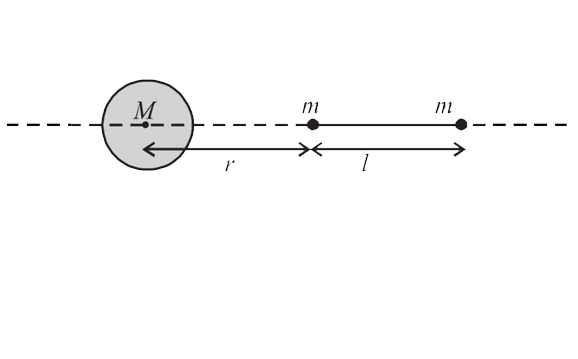
A larger spherical mass M is fixed at one position and two identical point masses m are kept on a line passing through the centre of M. The point masses are connected by rigid massless rod of length l and this assembly is free to move along the line connecting them. All three masses interact only throght their mutual gravitational interaction. When the point mass nearer to M is at a distance r =3l form M, the tensin in the rod is zero for m=k(M288). The value of k is
5
6
7
8
The correct Answer is:C
( c) Both the point masses are connected by a light rod so they have same acceleration.
Suppose each point mass is moving with acceleration a towards larger mass M.
Using Newton's 2nd law of motion for point mass nearer to larger mass,
F1−F=ma
GMm(3l)2−Gm2l2=ma ....(i)

Again using 2nd law of motion for another mass F2+F=ma
GMm(4l)2−Gm2l2=ma ....(ii)
From eqn. (i) and (ii), we get
GM9l2−Gml2=GM16l2+Gml2
M9−M16=m+m⇒7M144=2m
m=7M288=k(M288)∴k=7
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - NCERT Exemplear Problems.8videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion & Reason Corner15videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Question11videos
GRAVITATION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason10videos
KINETIC THEORY
Similar Questions
Find the potential V at P in the gravitational field of fixed point mass M.
View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
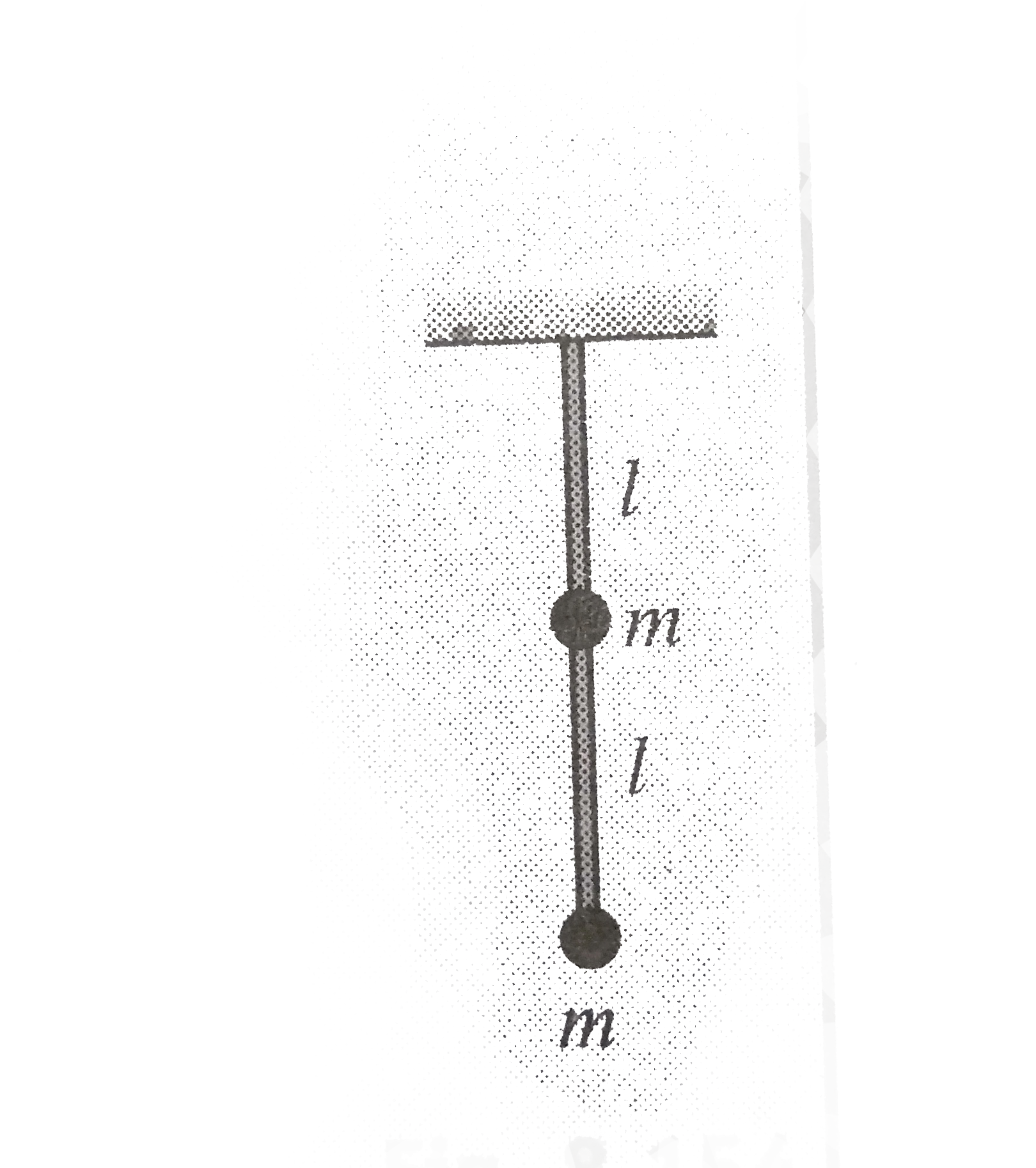 View Solution
View SolutionTwo particles of equal mass m0 are moving round a circle of radius r due to their mutual gravitational interaction. Find the time period of each particle.
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View SolutionTwo point masses m and 4 m are seperated by a distance d on a line . A third point mass m0 is to be placed at a point on the line such that the net gravitational force on it zero .

The distance of that point from the m mass isView SolutionTwo particles of masses m and 2m are placed at separation L. Find the M.I. about an axis passing through the center of mass and perpendicular to the line joining the point masses.
View SolutionTwo identical rods each of mass m and length are connected as shown. Locate c.m.
 View Solution
View SolutionTwo point masses m and 3m are placed at distance r. The moment of inertia of the system about an axis passing through the centre of mass of system and perpendicular to the joining the point masses is
View Solutiona point mass (m) is located at (0,a) where should th 2m mass be kept ,so that centre of mass lies at origin?
View SolutionTwo particles of masses 'm' and '9m' are separated by a distance 'r'. At a point on the line joining them the gravitational field is zero. The gravitational potential at that point is (G = Universal constant of gravitation)
View Solution

