For a perfectly rigid body
Young's modulus is infinite and bulk modulus is zero.
Young's modulus is zero and bulk modulus is infinite.
Young's modulus is infinite and bulk modulus is also infinite.
Young's modulus is zero and bulk modulus is also zero.
The correct Answer is:C
To solve the question regarding the properties of a perfectly rigid body, we need to analyze the definitions of Young's modulus and Bulk modulus and their implications for a rigid body.
1. Understanding Young's Modulus:
- Young's modulus (E) is defined as the ratio of stress (force per unit area) to strain (deformation/original length).
- Mathematically, it is given by:
E=StressStrain=F/AΔL/L0
- For a perfectly rigid body, when a force is applied, there is no deformation (strain = 0). Therefore, the strain approaches zero.
2. Calculating Young's Modulus for a Rigid Body:
- Since strain is zero, the formula for Young's modulus becomes:
E=F/A0→∞
- Hence, for a perfectly rigid body, Young's modulus is infinite.
3. Understanding Bulk Modulus:
- Bulk modulus (K) is defined as the ratio of change in pressure to the relative change in volume.
- Mathematically, it is given by:
K=−VdPdV
- For a perfectly rigid body, when pressure is applied, there is no change in volume (ΔV = 0).
4. Calculating Bulk Modulus for a Rigid Body:
- Since the change in volume is zero, the formula for Bulk modulus becomes:
K=−VdP0→∞
- Thus, for a perfectly rigid body, Bulk modulus is also infinite.
5. Conclusion:
- Both Young's modulus and Bulk modulus for a perfectly rigid body are infinite.
- Therefore, the correct answer to the question is: Young's modulus is infinite and Bulk modulus is infinite.
Final Answer:
- The correct option is: Young's modulus is infinite and Bulk modulus is also infinite.
- Young's modulus (E) is defined as the ratio of stress (force per unit area) to strain (deformation/original length).
- Mathematically, it is given by:
E=StressStrain=F/AΔL/L0
- For a perfectly rigid body, when a force is applied, there is no deformation (strain = 0). Therefore, the strain approaches zero.
- Since strain is zero, the formula for Young's modulus becomes:
E=F/A0→∞
- Hence, for a perfectly rigid body, Young's modulus is infinite.
- Bulk modulus (K) is defined as the ratio of change in pressure to the relative change in volume.
- Mathematically, it is given by:
K=−VdPdV
- For a perfectly rigid body, when pressure is applied, there is no change in volume (ΔV = 0).
- Since the change in volume is zero, the formula for Bulk modulus becomes:
K=−VdP0→∞
- Thus, for a perfectly rigid body, Bulk modulus is also infinite.
- Both Young's modulus and Bulk modulus for a perfectly rigid body are infinite.
- Therefore, the correct answer to the question is: Young's modulus is infinite and Bulk modulus is infinite.
- The correct option is: Young's modulus is infinite and Bulk modulus is also infinite.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - HOTS
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - STRESS-STRAIN CURVE
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
Which of the following is the vm = T graph for a perfectly black body ( vm =maximum frequency of radiation)
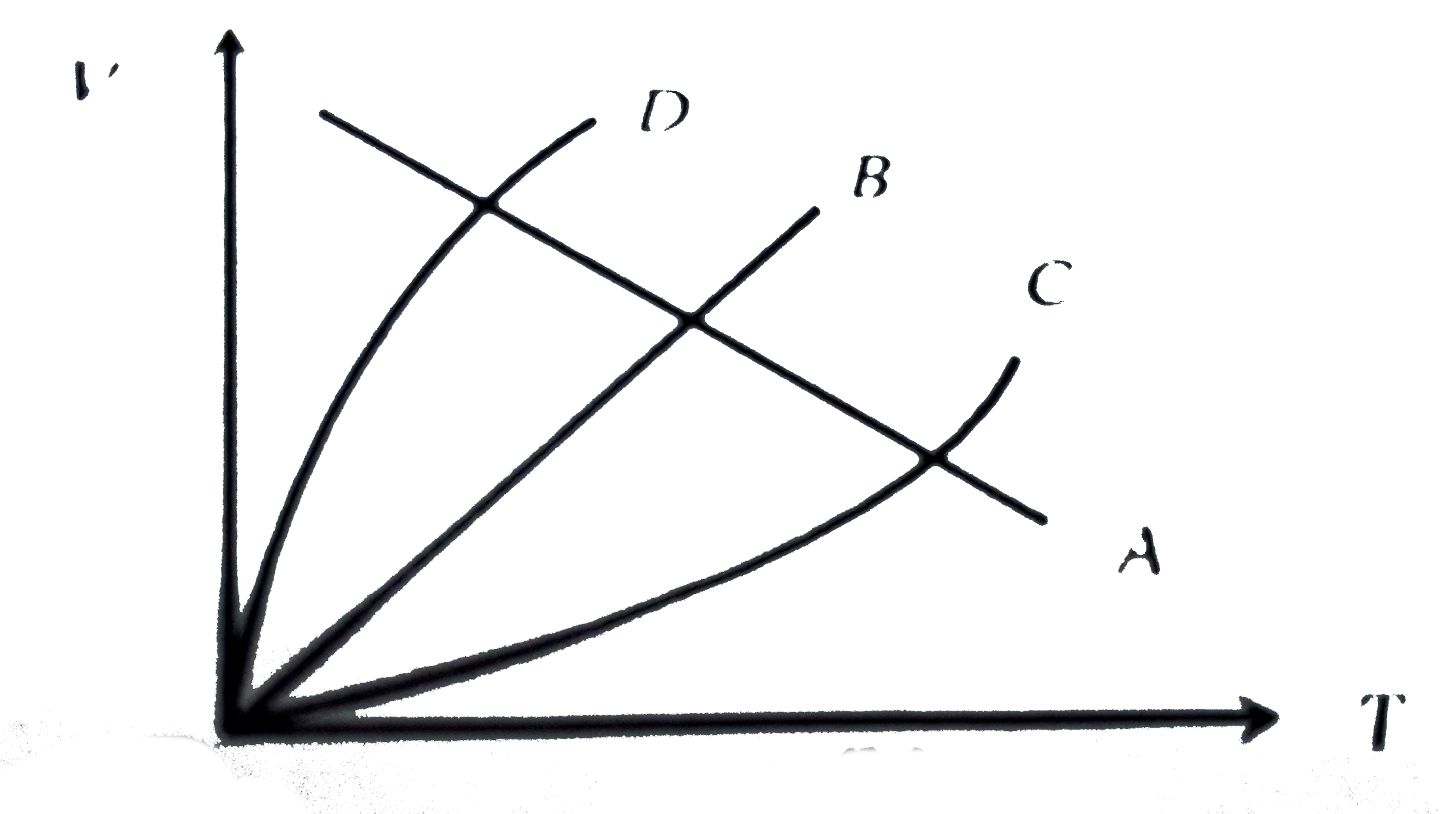 AABBCCDD
AABBCCDDIf the temperatures of a perfectly black body measured in Kelvin is doulbed, then the energy radiated per second becomes
Atwice the orginal valueB16 times the original valueChalf the original valueD4 times the original value
Statement-1: Young's modulus for a perfectly plastic body is zero
Statement-2: For a perfectly plastic body, restoring force is zero.
View SolutionFor perfectly black body emissivity (e) is
View SolutionThe reflectance and emittance of a perfectly black body are respectively
View SolutionThese question consists of two statements each printed as Assertion and Reason. While answering these question you are required to choose any one of the following five responses.
Assertion: Emissive power of a perfectly black body is one.
Reason: Absorptive power of perfectly black body is one.
View SolutionIf between wavelength λ andλ+dλ, eλ and aλ be the emissive and absorptive powers of a body and Eλ be the emissive power of a perfectly black body, then according to Kirchoff's law, which is true
View SolutionWhich one of the following is vm−T graph for perfectly black body ? vm is the frequency of radition with maximum intensity. T is the absolute temperature
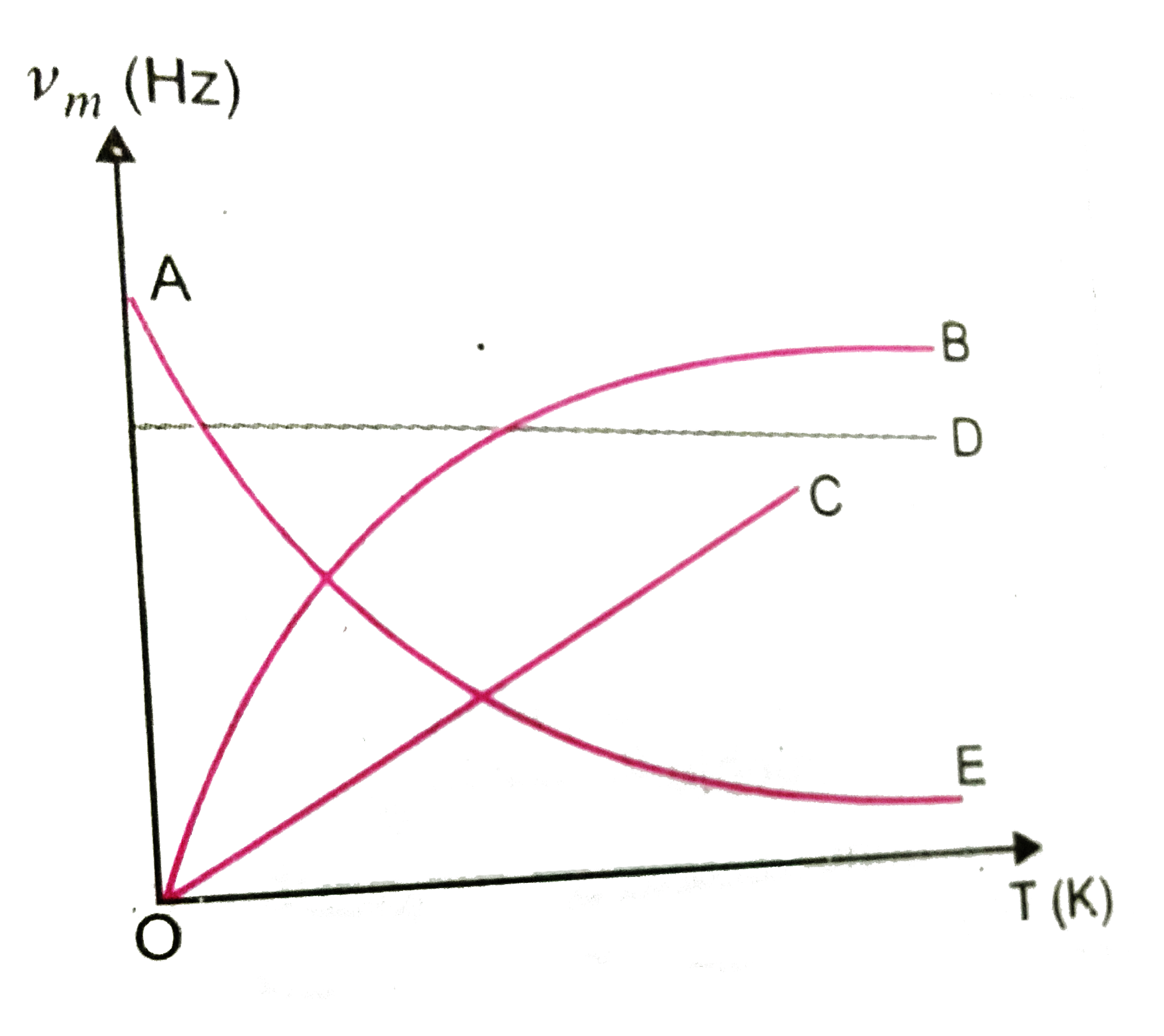
View Solution
