In an organ pipe of length L open at both ends, the fundamental mode has a frequency
(where v is a speed of sound in air)
v2L and only odd harmonies are present.
v2L and only even harmonies are present.
v2L and all harmonies are present.
v4L and only odd harmonies are present.
The correct Answer is:C
To find the fundamental frequency of an organ pipe of length L that is open at both ends, we can follow these steps:
1. Understand the Pipe Configuration:
- An organ pipe that is open at both ends supports standing waves with antinodes at both ends. This means that the fundamental frequency corresponds to the simplest standing wave pattern.
2. Determine the Wavelength:
- For a pipe open at both ends, the fundamental mode (first harmonic) has a wavelength λ such that the length of the pipe L is equal to half the wavelength:
L=λ2
- Rearranging this gives:
λ=2L
3. Use the Wave Speed Formula:
- The frequency f of a wave is related to its speed v and wavelength λ by the formula:
f=vλ
4. Substitute the Wavelength:
- Substitute λ=2L into the frequency formula:
f=v2L
5. Conclusion:
- Therefore, the fundamental frequency f of the organ pipe is:
f=v2L
Final Answer:
The fundamental frequency of an organ pipe of length L open at both ends is given by:
f=v2L
- An organ pipe that is open at both ends supports standing waves with antinodes at both ends. This means that the fundamental frequency corresponds to the simplest standing wave pattern.
- For a pipe open at both ends, the fundamental mode (first harmonic) has a wavelength λ such that the length of the pipe L is equal to half the wavelength:
L=λ2
- Rearranging this gives:
λ=2L
- The frequency f of a wave is related to its speed v and wavelength λ by the formula:
f=vλ
- Substitute λ=2L into the frequency formula:
f=v2L
- Therefore, the fundamental frequency f of the organ pipe is:
f=v2L
The fundamental frequency of an organ pipe of length L open at both ends is given by:
f=v2L
Topper's Solved these Questions
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - HOTS
8 Videos
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - EXEMPLER
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - Assertion And Reason
15 Videos
Similar Questions
Show that an organ pipe of length 2l open at both ends has the same fundamental frequency as another pipe of length I closed at one end.
View SolutionAn organ pipe, open at both ends, contains
View SolutionThe length of an organ pipe open at both ends is 0.5 m. Calculate the fundamental frequency of the pipe, if the velocity of sound in air be 350 m/s. If one end of the pipe is closed then what will be the fundamental frequency ?
View SolutionAn open organ pipe of length L vibrates in its fundamental mode. The pressure variation is maximum
View SolutionThe length of a pipe open at both ends is 48 cm and its fundamental frequency is 320 Hz. If the speed of sound be 320ms−1 then determine the diameter of the pipe. If one end of the pipe be closed, then what will be the fundamental frequency?
View SolutionAn open pipe of sufficient length is dipping in water with a speed v vertically. If at any instant l is lengths of tube avoce water. Then the rate at which fundamental frequency of pipe changes , is ( speed of sound = c)
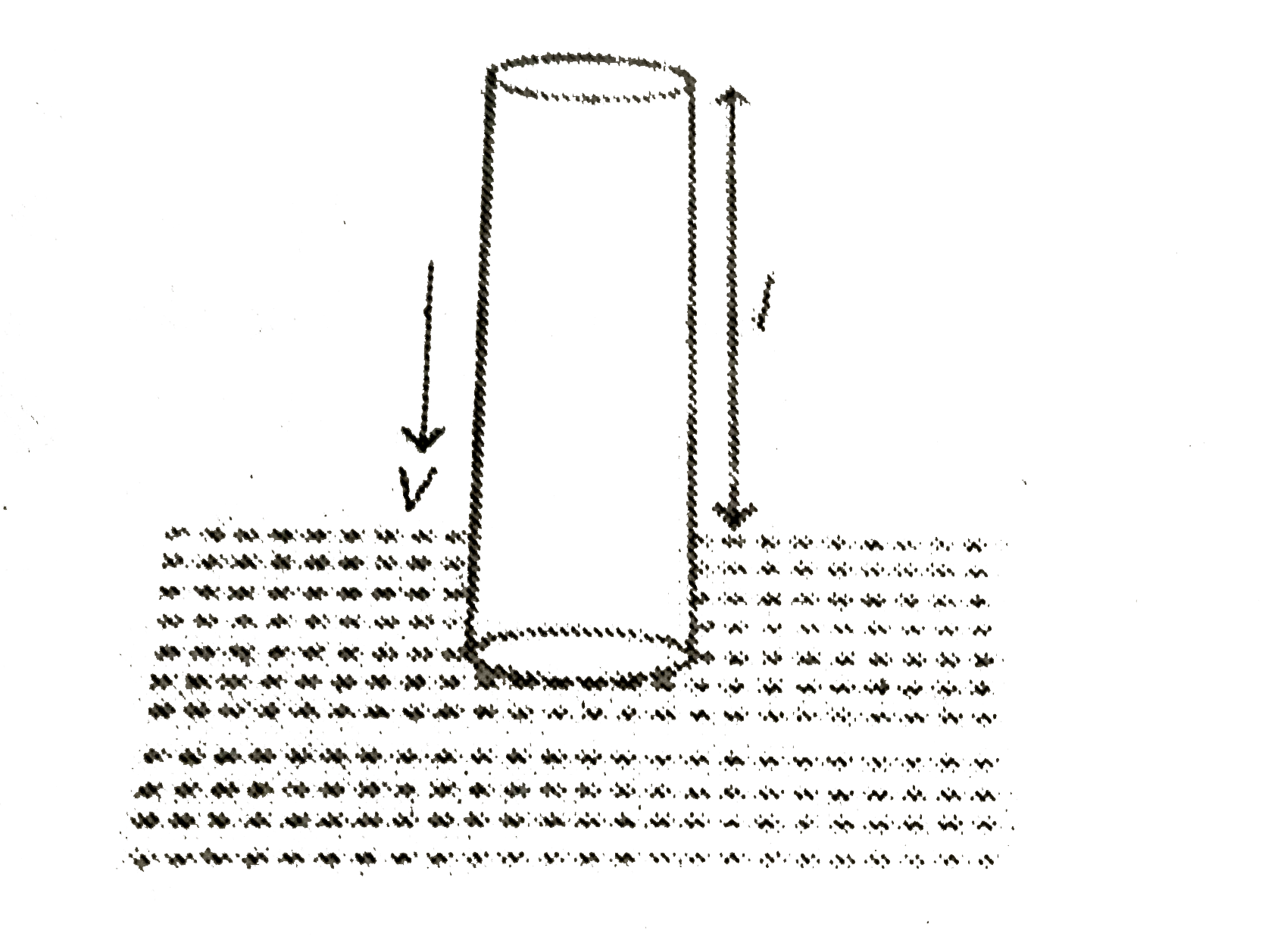
View SolutionAn open organ pipe of length 11cm in its fundamental mode vibrates in resonance with the first overtone of a closed organ pipe of length 13.2cm filled with some gas . If the velocity of sound in air is 330m/s, calculate the velocity of sound in the unknown gas .
View SolutionAn organ pipe closed at one end has a length 1m and an open organ pipe has a length 1.6 m . The speed of sound in air is 320 m/s . The two pipes can resonates for a sound of frequency
View SolutionWhen the open organ pipe resonates in its fundamental mode then at the centre of the pipe
View SolutionA flute which we treat as a pipe open at both ends is 60cm long. (a) What is the fundamental frequency when all the holes are covered? (b) How far from the mouthpieces should a hole be uncovered for the fundamental frequency to be 330HZ ? Take speed of sound in air as 340m/s.
View Solution
