A planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
R2/r2
r2/R2
R/r
r/R
The correct Answer is:C
To solve the problem, we will use the principle of conservation of angular momentum. The angular momentum of a planet revolving around the Sun is given by the product of its mass, its velocity, and its distance from the Sun.
1. Identify the positions and velocities:
- The closest distance from the Sun (perihelion) is r with velocity v.
- The farthest distance from the Sun (aphelion) is R with velocity V.
2. Write the expression for angular momentum:
- Angular momentum at the closest point (perihelion) is given by:
Lperihelion=M⋅v⋅r
- Angular momentum at the farthest point (aphelion) is given by:
Laphelion=M⋅V⋅R
Here, M is the mass of the planet.
3. Apply the conservation of angular momentum:
- Since there are no external torques acting on the planet-sun system, the angular momentum at perihelion must equal the angular momentum at aphelion:
M⋅v⋅r=M⋅V⋅R
4. Cancel the mass M:
- Since M is present on both sides of the equation, we can cancel it out:
v⋅r=V⋅R
5. Rearrange the equation to find the ratio vV:
- We can rearrange the equation to express the ratio of the velocities:
vV=Rr
6. Conclusion:
- Therefore, the ratio of the velocity of the planet at its closest distance to the velocity at its farthest distance is:
vV=Rr
Final Answer:
The ratio vV is Rr.
- The closest distance from the Sun (perihelion) is r with velocity v.
- The farthest distance from the Sun (aphelion) is R with velocity V.
- Angular momentum at the closest point (perihelion) is given by:
Lperihelion=M⋅v⋅r
- Angular momentum at the farthest point (aphelion) is given by:
Laphelion=M⋅V⋅R
Here, M is the mass of the planet.
- Since there are no external torques acting on the planet-sun system, the angular momentum at perihelion must equal the angular momentum at aphelion:
M⋅v⋅r=M⋅V⋅R
- Since M is present on both sides of the equation, we can cancel it out:
v⋅r=V⋅R
- We can rearrange the equation to express the ratio of the velocities:
vV=Rr
- Therefore, the ratio of the velocity of the planet at its closest distance to the velocity at its farthest distance is:
vV=Rr
The ratio vV is Rr.
Topper's Solved these Questions
Similar Questions
A planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R. If the orbital velocity of the planet closest to the Sun is v, then what is the velocity at the farthest point?
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the sun is rmin. The farthest distance from the sun is rmax if the orbital angular velocity of the planet when it is nearest to the Sun ω then the orbital angular velocity at the point when it is at the farthest distance from the sun is
View Solution
Knowledge Check
A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
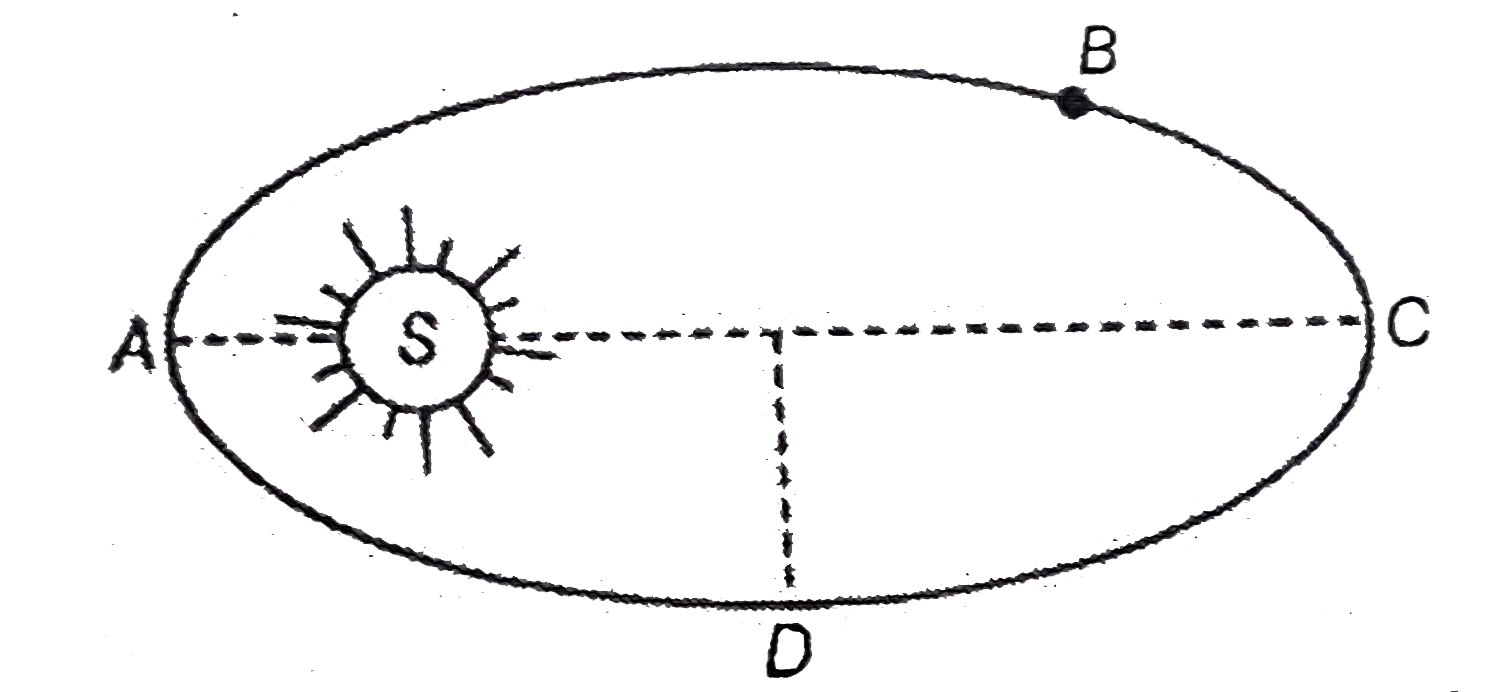 AABBCCDD
AABBCCDD
A planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
View SolutionWhich planet is farthest to Sun ?
View SolutionA planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at

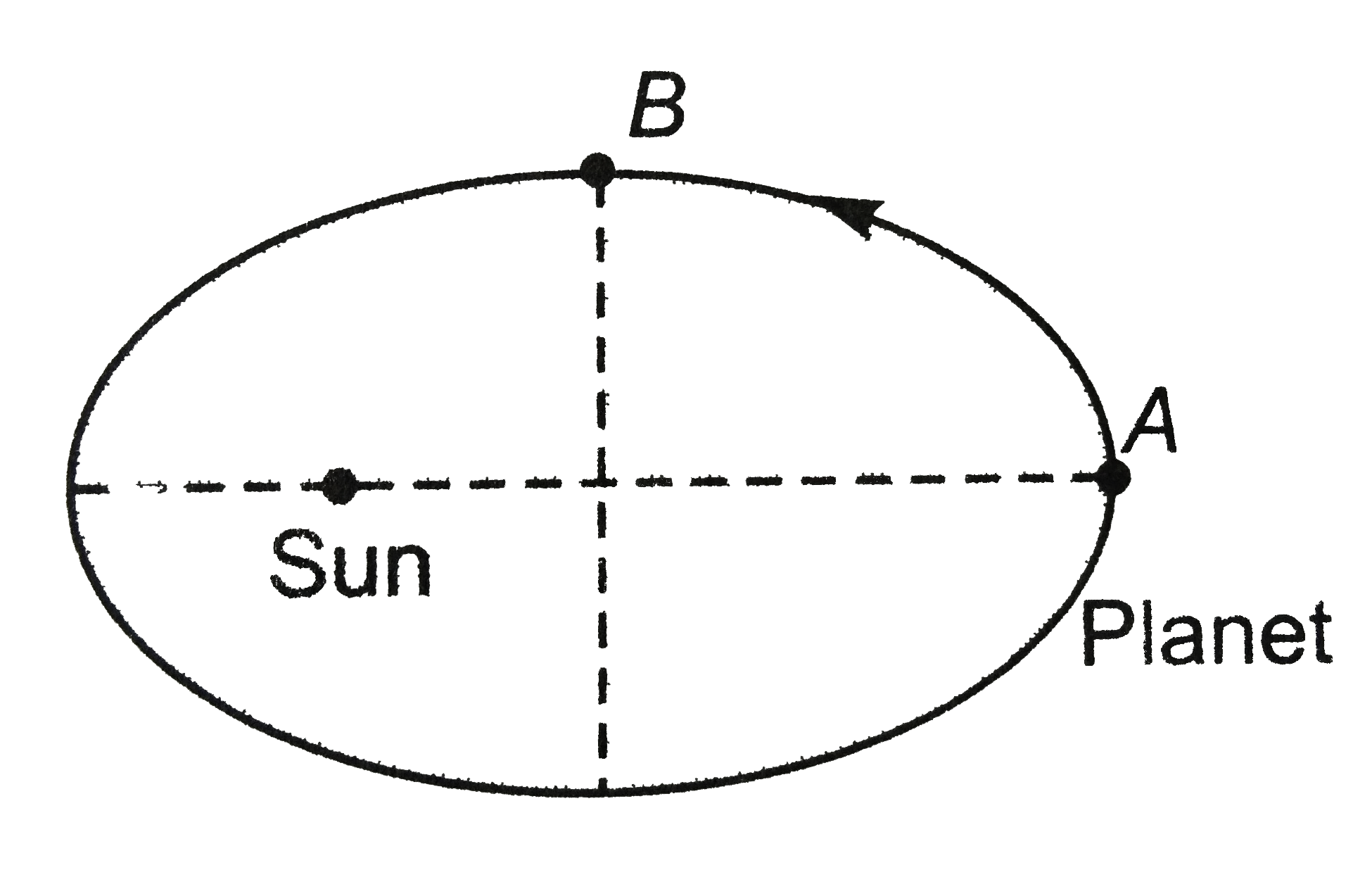
View SolutionA planet is moving round the sun in an elliptical orbit as shows. As the planet moves from A to B
View SolutionConsider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
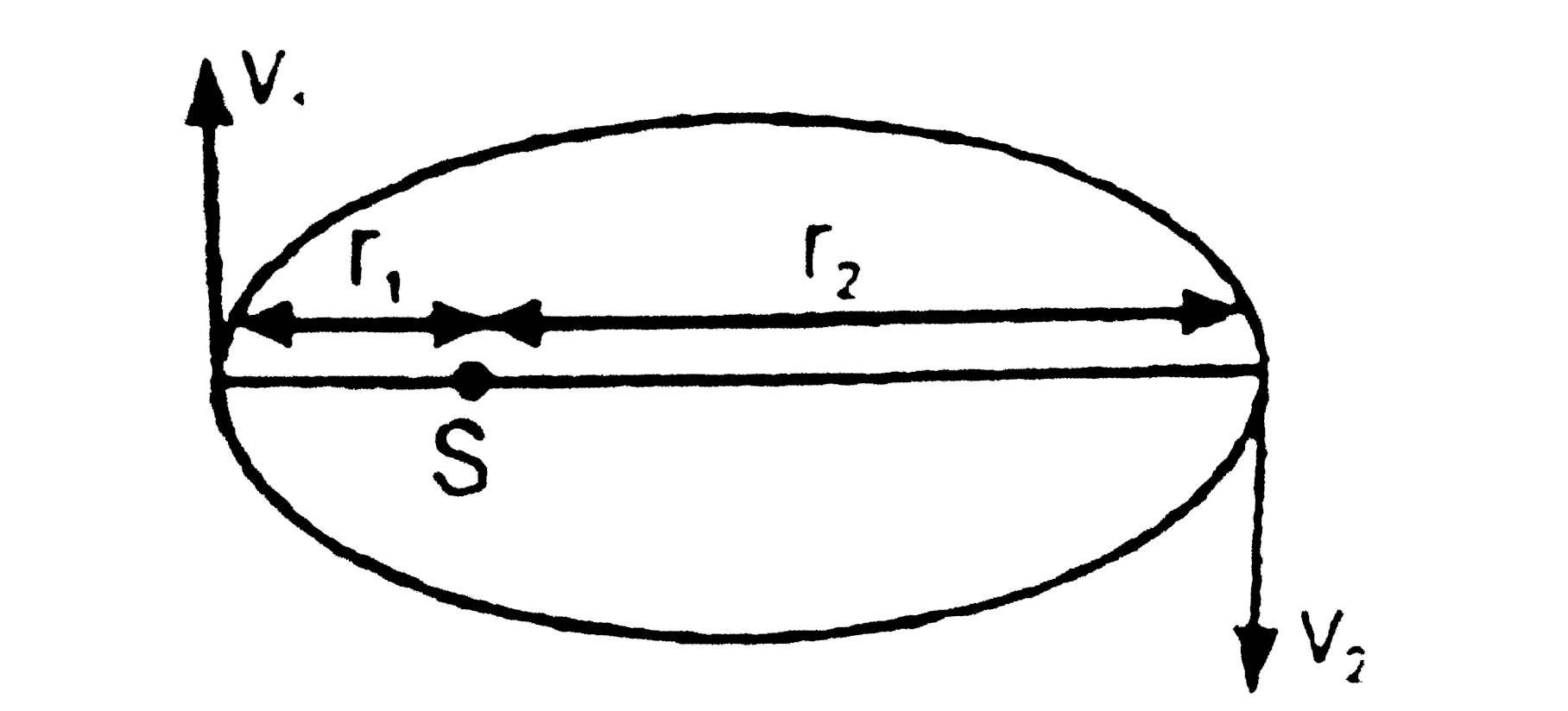
View SolutionA planet is revolving in an elliptical orbit around the sun as shown in the figure. The areal velocity (area swapped by the radius vector with respect to sun in unit time) is:
View SolutionConsider a planet moving in an elliptical orbit round the sun. The work done on the planet by the gravitational force of the sun
View Solution
