An alternating current generator has an internal resistance Rg and an internal reactance Xg. It is used to supply power to a passive load consisting of a resistance Rg and a rectance XL. For maximum power to be delivered from the generator to the load, the value of XL is equal to
zero
Xg
−Xg
Rg
The correct Answer is:C
To solve the problem of finding the value of XL for maximum power transfer from the alternating current generator to the load, we can follow these steps:
1. Understand the Components:
- The generator has an internal resistance Rg and an internal reactance Xg.
- The load consists of a resistance RL (which is equal to Rg) and a reactance XL.
2. Condition for Maximum Power Transfer:
- For maximum power transfer in an AC circuit, the total reactance must be zero. This means that the reactance of the generator and the load must cancel each other out.
3. Set Up the Equation:
- The condition for maximum power transfer can be expressed as:
Xg+XL=0
4. Solve for XL:
- Rearranging the equation gives:
XL=−Xg
5. Conclusion:
- Therefore, the value of XL for maximum power transfer is equal to the negative of the internal reactance of the generator:
XL=−Xg
Final Answer:
The value of XL is −Xg.
---
- The generator has an internal resistance Rg and an internal reactance Xg.
- The load consists of a resistance RL (which is equal to Rg) and a reactance XL.
- For maximum power transfer in an AC circuit, the total reactance must be zero. This means that the reactance of the generator and the load must cancel each other out.
- The condition for maximum power transfer can be expressed as:
Xg+XL=0
- Rearranging the equation gives:
XL=−Xg
- Therefore, the value of XL for maximum power transfer is equal to the negative of the internal reactance of the generator:
XL=−Xg
The value of XL is −Xg.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - ASSERTION & REASON15videos
ALTERNATING CURRENT
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Ac Voltage Applied To A Resistor17videos
ALTERNATING CURRENT
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - HOTS8videos
ALTERNATING CURRENT
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ATOMS EXERCISE - Assertion And Reason15videos
ATOMS
Similar Questions
A cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
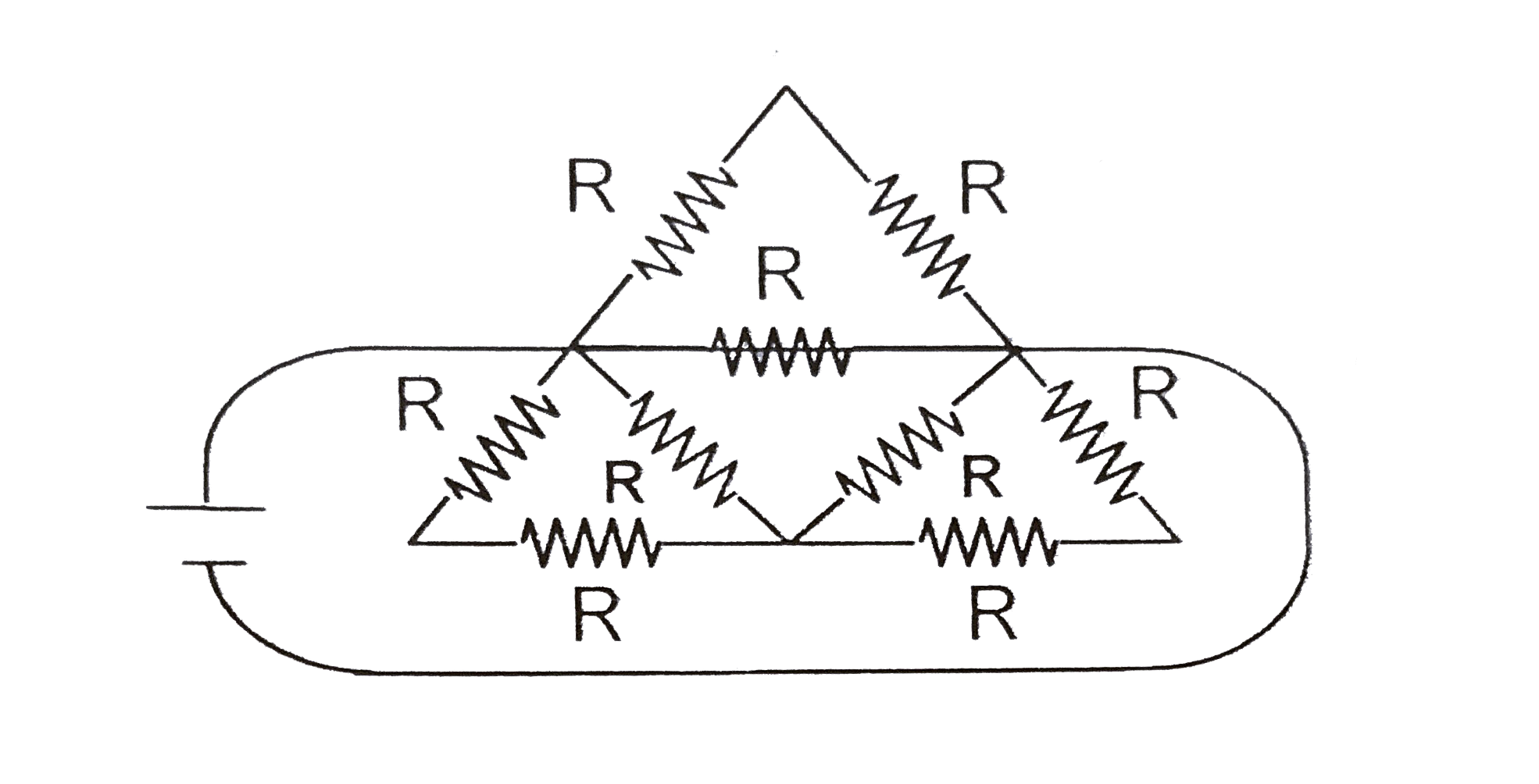
.View SolutionA battery of internal resistance 4Ω is connected to the network of resistance as shown . In order that the maximum power can be delivered to the network, the value of R in Ω should be
 . View Solution
. View SolutionIn the situation shown each cell has e.m.f. 4V and internal resistance 1Ω. The maximum power that can be delivered to the variable load resistance R is
 View Solution
View SolutionA battery is of emt E and internal resistance R. The value of external resistance r so that the power across eternal resistance is maximum :
View SolutionFor maximum power from battery the internal resistance of battery r is
 View Solution
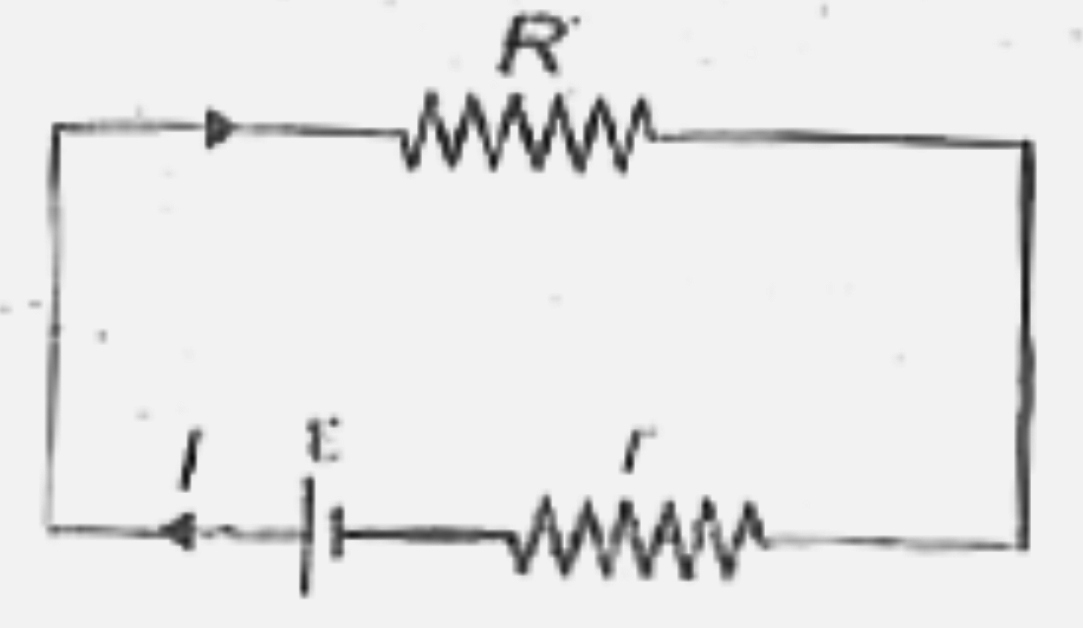
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R .
(i) Find the maximum power delivered at the load ?
(ii) Draw the power (P) vs load resistance (R) graph .
 View Solution
View SolutionA power supply with an e.m.f ε and internal resustance r is connected to a variable resistance R. Find the dependence of the total power generated by the supply and of the power delivered to the external circuit on the load resistance.
View SolutionA cell of emf 16V and internal resistant 4Ω can deliver maximum power to a load of resistance R where R is equal to
View SolutionA cell of internal resistance r drivers current through an external resistance R. The power delivered by the to the external resistance will be maximum when:
View SolutionTwo cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View Solution

