Light of wavelength λ falls on metal having work functions hc/λ0 . Photoelectric effect will take place only if :
λ≥λ0
λ≤λ0
λ≥2λ0
λ=4λ0
The correct Answer is:B
To solve the problem, we need to analyze the conditions under which the photoelectric effect occurs when light of wavelength λ falls on a metal with a work function given by hcλ0.
1. Understanding the Photoelectric Effect:
The photoelectric effect occurs when light falls on a metal surface and ejects electrons from it. For this to happen, the energy of the incoming photons must be greater than or equal to the work function of the metal.
2. Using Einstein's Photoelectric Equation:
According to Einstein's photoelectric equation:
E=hν=Work Function+Kinetic Energy
where E is the energy of the incoming photon, h is Planck's constant, ν is the frequency of the light, and the work function is the minimum energy required to eject an electron.
3. Relating Frequency to Wavelength:
The frequency ν can be expressed in terms of wavelength λ as:
ν=cλ
where c is the speed of light. Therefore, the energy of the photon can be rewritten as:
E=hν=hcλ
4. Substituting the Work Function:
The work function ϕ is given as:
ϕ=hcλ0
Thus, the condition for the photoelectric effect to occur can be written as:
hcλ≥hcλ0
5. Simplifying the Inequality:
Dividing both sides by hc (which is positive), we get:
1λ≥1λ0
This can be rearranged to:
λ0≥λ
6. Final Result:
Therefore, the condition for the photoelectric effect to take place is:
λ≤λ0
Conclusion:
The photoelectric effect will take place only if the wavelength λ of the incident light is less than or equal to the threshold wavelength λ0.
The photoelectric effect occurs when light falls on a metal surface and ejects electrons from it. For this to happen, the energy of the incoming photons must be greater than or equal to the work function of the metal.
According to Einstein's photoelectric equation:
E=hν=Work Function+Kinetic Energy
where E is the energy of the incoming photon, h is Planck's constant, ν is the frequency of the light, and the work function is the minimum energy required to eject an electron.
The frequency ν can be expressed in terms of wavelength λ as:
ν=cλ
where c is the speed of light. Therefore, the energy of the photon can be rewritten as:
E=hν=hcλ
The work function ϕ is given as:
ϕ=hcλ0
Thus, the condition for the photoelectric effect to occur can be written as:
hcλ≥hcλ0
Dividing both sides by hc (which is positive), we get:
1λ≥1λ0
This can be rearranged to:
λ0≥λ
Therefore, the condition for the photoelectric effect to take place is:
λ≤λ0
The photoelectric effect will take place only if the wavelength λ of the incident light is less than or equal to the threshold wavelength λ0.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - EINSTEIN S PHOTOELECTRIC EQUATION : ENERGY QUANTUM OF RADIATION23videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - PARTICLE NATURE OF LIGHT : THE PHOTON19videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - PHOTOELECTRIC EFFECT2videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion And Reason15videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason15videos
ELECTRIC CHARGES AND FIELDS
Similar Questions
The work function of a metal is hv0. Light of frequency v falls on this metal. The photoelectric effect will take place only if
View SolutionA metal has a work function ϕ0 and its corresponding threshold wavelength is λ0. If the threshold wavelength for a metal whose work function is ϕ03 is nλ0, then what is the value of n ?
View SolutionThe graph between 1/λ and stopping potential (V) of three metals having work- functions Φ1, Φ2 and Φ3 in an experiment of photoelectric effect is plotted as shown in the figure. Which of the following statement(s) is/are correct? (Here, λ is the wavelength of the incident ray).
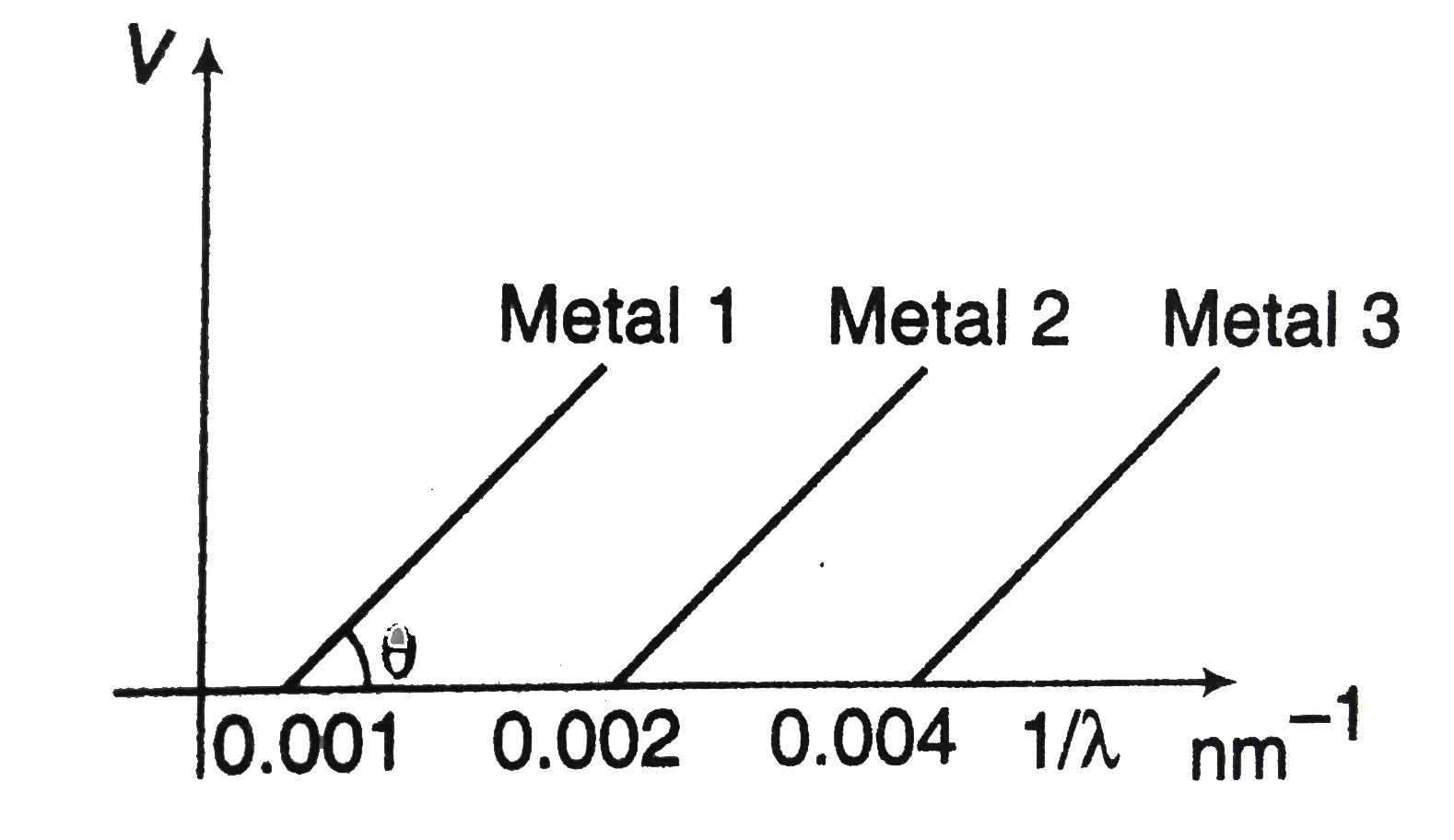 View Solution
View SolutionLight of wavelength λ is incident on metal surface. Work function of metal is very small compare to kinetic energy of photon. If light of wave length λ' is incident on metal surface then linear momentum of electron becomes 1.5 of initial, find out λ'.
View SolutionLight of wavelength 2000 Å falls on a metallic surface whose work function is 4.21 eV. Calculate the stopping potential
View SolutionLight of energy 2.0 eV falls on a metal of work function 1.4 eV . The stopping potential is
View SolutionIf light of wavelength λ1 is allowed to fall on a metal , then kinetic energy of photoelectrons emitted is E1. If wavelength of light changes to λ2 then kinetic energy of electrons changes to E2. Then work function of the metal is
View SolutionIf the threshold wavelength (λ0) for ejection of electron from metal is 330 nm, then work function for the photoelectric emission is:
View SolutionThe maximum velocity of an electron emitted by light of wavelength λ incident on the surface of a metal of work function ϕ, is
Where h = Planck's constant , m = mass of electron and c = speed of light.View SolutionWhen light of wavelength λ is incident on a metal surface, stopping potential is found to be x. When light of wavelength nλ is incident on the same metal surface, stopping potential is found to be xn+1 . Find the threshold wavelength of the metal.
View Solution

