If the whole earth is to be connected by LOS communication using space waves ( no restriction of antenna size or tower height), what is the minimum no of antennaas required ? Calculate the tower height of these antennas in terms of earth's radius?
2
3
4
6
The correct Answer is:D
To solve the problem of connecting the whole Earth using line-of-sight (LOS) communication with antennas, we will follow these steps:
Step 1: Understand the Geometry
We start by visualizing the Earth as a sphere with a radius r. We need to place antennas on the surface of the Earth such that they can communicate with each other using space waves.
Step 2: Determine the Line of Sight Distance
The maximum distance dm for line-of-sight communication can be derived using the Pythagorean theorem. If we have an antenna at height ht above the Earth's surface, the distance to the horizon (line of sight) can be expressed as:
dm=√2htr
where r is the radius of the Earth.
Step 3: Set Up the Antenna Height
Assuming the height of the transmitting and receiving antennas is the same, we can denote the height as ht. For effective communication, we need to ensure that the antennas can cover the entire surface of the Earth.
Step 4: Calculate the Required Number of Antennas
To cover the entire surface of the Earth, we need to consider the geometry of the sphere. The surface area A of the Earth is given by:
A=4πr2
If we place antennas at equal distances apart, we can visualize that each antenna covers a circular area on the surface. The area covered by one antenna can be approximated based on the distance dm.
Step 5: Determine the Height of the Antennas
From the previous steps, we derived that:
dm=√2htr
To ensure that the antennas can communicate effectively, we can set ht=r. This means that the height of the antennas is equal to the radius of the Earth.
Step 6: Calculate the Minimum Number of Antennas
If we assume that each antenna can cover a circular area with a radius dm, the area covered by one antenna can be expressed as:
Aantenna=πd2m=π(2htr)=2πh2tr
Given that ht=r, we can substitute this into the area formula:
Aantenna=2πr3
Now, to find the minimum number of antennas N required to cover the entire surface area of the Earth, we can divide the total surface area by the area covered by one antenna:
N=AAantenna=4πr22πr3=42r=2r
However, since we need to cover the entire Earth, we find that we need 6 antennas to ensure full coverage.
Final Result
Thus, the minimum number of antennas required is 6, and the height of these antennas in terms of the Earth's radius is:
ht=r
We start by visualizing the Earth as a sphere with a radius r. We need to place antennas on the surface of the Earth such that they can communicate with each other using space waves.
The maximum distance dm for line-of-sight communication can be derived using the Pythagorean theorem. If we have an antenna at height ht above the Earth's surface, the distance to the horizon (line of sight) can be expressed as:
dm=√2htr
where r is the radius of the Earth.
Assuming the height of the transmitting and receiving antennas is the same, we can denote the height as ht. For effective communication, we need to ensure that the antennas can cover the entire surface of the Earth.
To cover the entire surface of the Earth, we need to consider the geometry of the sphere. The surface area A of the Earth is given by:
A=4πr2
If we place antennas at equal distances apart, we can visualize that each antenna covers a circular area on the surface. The area covered by one antenna can be approximated based on the distance dm.
From the previous steps, we derived that:
dm=√2htr
To ensure that the antennas can communicate effectively, we can set ht=r. This means that the height of the antennas is equal to the radius of the Earth.
If we assume that each antenna can cover a circular area with a radius dm, the area covered by one antenna can be expressed as:
Aantenna=πd2m=π(2htr)=2πh2tr
Given that ht=r, we can substitute this into the area formula:
Aantenna=2πr3
Now, to find the minimum number of antennas N required to cover the entire surface area of the Earth, we can divide the total surface area by the area covered by one antenna:
N=AAantenna=4πr22πr3=42r=2r
However, since we need to cover the entire Earth, we find that we need 6 antennas to ensure full coverage.
Thus, the minimum number of antennas required is 6, and the height of these antennas in terms of the Earth's radius is:
ht=r
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - HOTS20videos
COMMUNITCATION SYSTEMS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - NCERT9videos
COMMUNITCATION SYSTEMS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ATOMS EXERCISE - Assertion And Reason15videos
ATOMS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Assertion And Reason15videos
CURRENT ELECTRICITY
Similar Questions
Name the type of waves which are used for line of sight (LOS) communication. What is the range of their frequencies?
A transmitting antenna at the top of a tower has a height of 20m and the height of the receiving antenna is 45m. Calculate the maximum distance between them for satisfactory communication in LOS mode. (Radius of the Earth =6.4×106 m)View SolutionThe radius of the Earth is 6400 km. If the height of an antenna is 500 m, then its range is
View Solution
Knowledge Check
- Question 1 - Select One
A satellite is to be placed in equatorial geostationary orbit around the earth for communication.
(a) Calculate height of such a satellite
(b) Find out the minimum number of satellites that are needed to cover entire earth, so that atleast one satellite is visible from any point on the equator.
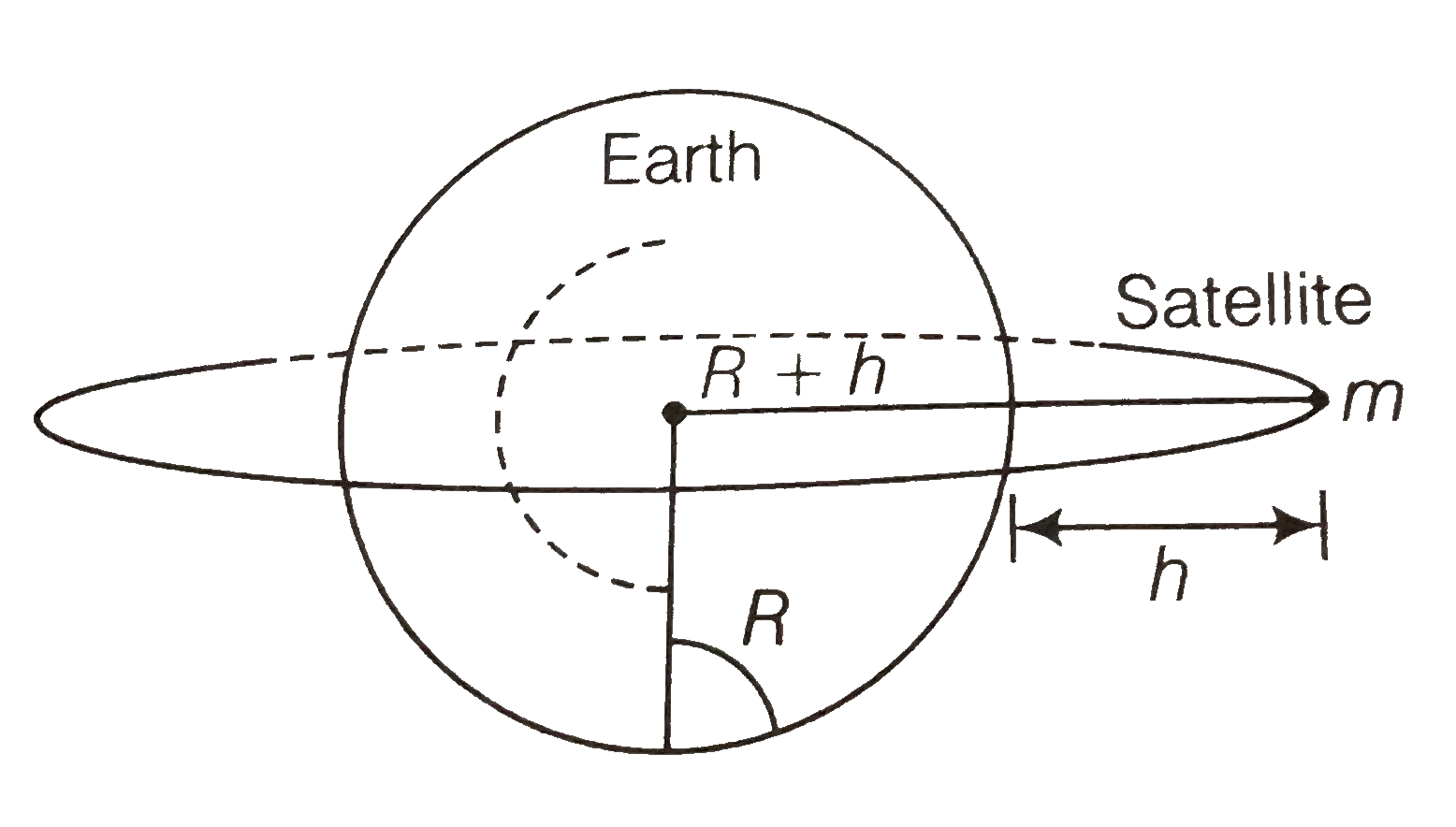
[M=6×1024kg,R=6400km,T=24h,G=6.67×10−11 SI unit ]A3.57×105mB3.57×106mC3.57×107mD3.57×108m
In a line of sight radio communication, a distance of about 50 is Kept between the transmitting and receiving entennas. If the height of the receiving antenna is 70m , then the minimum height fof the transmitting antenna should be:
(Radius of the Earth=6.4×106m).View SolutionWhat does the term LOS communication mean? Name the types of waves that are used for this communication. Which of the two height of transmitting antenna and height of receiving antenna can effect the range over which this mode of communication remains effective?
View SolutionWhat is line of sight communication? Why is it not possible to use sky waves for transmission of T.V. signals? Upto what distance can a signal be transmitted using an antenna of height h?
View SolutionA satellite is to be put into an orbit 600km above the surface of the earth. If its vertical velocity after launching is 2400m/s at this height, calculate the magnitude and direction in the impulse required to put the satellite directly increase. The mass of the satellite is 60kg and the radius of the earth is 6400km. Take g=10ms−2
View SolutionA satellite is to be placed in equatorial geostationary orbit around earth for communication.
(a) Calculate height of such a satellite.
(b) Find out the minimum number of satellites that are needed to cover entire earth so that at least one satellites is visible from any point on the equator.
[M=6×1024kg,R=6400km,T=24h,G=6.67×10−11SIunits]View SolutionA TV transmission tower of antenna is at a height of 20 m. How much service area can it cover if the receiving antenna is (i) at ground level (ii) at a height of 25 m ? Calculate the percentage increase in area covered in case (ii) relative to case (i). Radius of earth =6.4×106m
View SolutionA conducting bolloon of the radius a is charged to potential V0 and held at a large height above the earth ensures that charge distribution on the surface of the balloon remains unaffected by the presence of the earth. It is connected to the earth through a resistance R and a value in the balloon is opened . The gas inside the balloon escapes from value and the size of the balloon decreases. The rate of decrease in radius of the balloon is controlled in such a manner that potential of the balloon remains constant. Assume the electric permittivity of the surrounding air equals to that of free space (ε0) and charge cannot leak to the surrounding air.
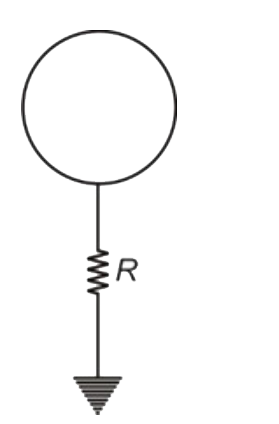
The rate at which radius r of the balloon changes with time is best represented by the equationView Solution

