A tree is 18.0m away from 2.0m high from a concave lens. How high is the image formed by the given lens of focal length 6m ?
1.0m
1.5m
0.75m
0.50m
The correct Answer is:D
To solve the problem step by step, we will use the lens formula and the magnification formula.
Step 1: Identify the given parameters
- Distance of the object (tree), u=−18.0m (negative because it is on the same side as the incoming light)
- Height of the object (tree), ho=2.0m
- Focal length of the concave lens, f=−6.0m (negative for concave lenses)
Step 2: Use the lens formula
The lens formula is given by:
1f=1v−1u
Substituting the known values:
1−6=1v−1−18
This simplifies to:
1−6=1v+118
Step 3: Rearranging to find v
To isolate 1v, we can rearrange the equation:
1v=1−6−118
Finding a common denominator (which is 18):
1v=−318−118=−418
Thus,
1v=−29
Taking the reciprocal gives:
v=−92=−4.5m
Step 4: Calculate the magnification
The magnification m is given by:
m=hiho=vu
Substituting the values we have:
m=−4.5−18=14
Step 5: Find the height of the image
Using the magnification to find the height of the image:
hi=m⋅ho=14⋅2.0m=0.5m
Final Answer
The height of the image formed by the concave lens is 0.5m.
---
- Distance of the object (tree), u=−18.0m (negative because it is on the same side as the incoming light)
- Height of the object (tree), ho=2.0m
- Focal length of the concave lens, f=−6.0m (negative for concave lenses)
The lens formula is given by:
1f=1v−1u
Substituting the known values:
1−6=1v−1−18
This simplifies to:
1−6=1v+118
To isolate 1v, we can rearrange the equation:
1v=1−6−118
Finding a common denominator (which is 18):
1v=−318−118=−418
Thus,
1v=−29
Taking the reciprocal gives:
v=−92=−4.5m
The magnification m is given by:
m=hiho=vu
Substituting the values we have:
m=−4.5−18=14
Using the magnification to find the height of the image:
hi=m⋅ho=14⋅2.0m=0.5m
The height of the image formed by the concave lens is 0.5m.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Reflection Of Light By Spherical Mirrors5videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Refraction10videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON15videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 350videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason15videos
SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS
Similar Questions
Find the power of a concave lens of focal length 2m.
View SolutionA thin converging lens forms a real image of an object located far away from the lens. The image is formed at A at a distance 4x from the lens and height of the image is h. A thin diverging lens of focal length x is placed at B[PB=2x] and a converging lens of focal length 2x is placed at C[PC=3x]. The principal axes of all lenses coincide. Find the height of the final image formed.
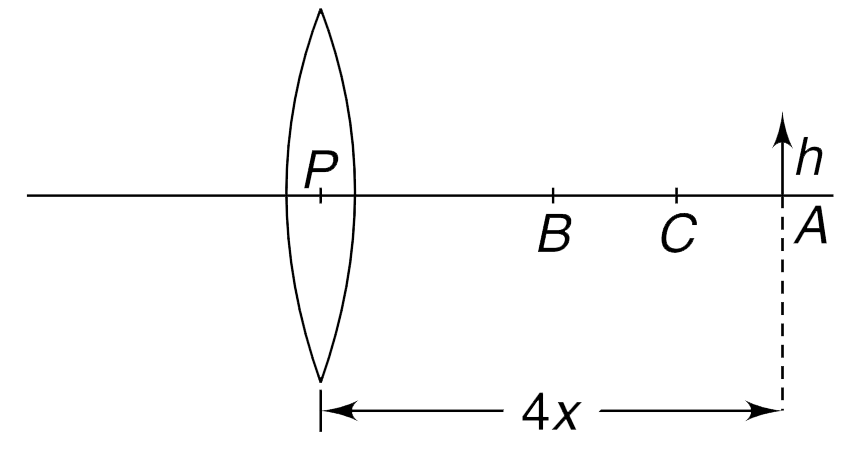 View Solution
View SolutionAn object is kept at a distance of 16cm from a thin lens and the image formed is real. If the object is kept at a distance of 6cm from the lens, the image formed is virtual. If the sizes of the images formed are equal, the focal length of the lens will be
View SolutionWhen an object is placed 40cm from a diverging lens, its virtual image is formed 20cm from the lens. The focal length and power of lens are
View SolutionA convex lens of focal length 30 cm , a concave lens of focal length 120 cm , and a plane mirror are arranged as shown . For an object kept at a distance of 60 cm from the convex lens, the final image, formed by the combination , is a real image , at a distance of :
_E01_195_Q01.png)
|Focal length|=|Focal length|
= 30cm =120cm
_S01_267_Q02.png) View Solution
View SolutionA convex lens produces an image of a real object on a screen with a magnification of 1/2. When the lens is moved 30 cm away from the object, the magnification of the image on the screen is 2. The focal length of the lens is
View SolutionAn object is placed at a distance of 40 cm from a convex lens of focal length 20cm. On the far side of the lens, a concave mirror of focal length 10cm is placed such that the distance of the object from the concave mirror is 100 cm. Then the final image which is formed after refraction from the lens, reflection from the mirror and again refraction from the lens, will be
View SolutionThe radius of the sun is 0.75×108m and its distance from the earth is 1.5×1011m. Find the diameter of the image of the sun formed by a lens of focal length 40cm
View SolutionAn object of size 3.0cm is placed 14cm in front of a concave lens of focal length 21cm. Describe the image produced by the lens. What happens if the object is moved further from the lens ?
View SolutionAn object of size 3.0cm is placed 14cm in front of a concave lens of focal length 21cm. Describe the image produced by the lens. What happens if the object is moved further from the lens ?
View Solution

