A point moves with a uniform acceleration and v1,v2,v3 denote the average velociies in the three succellive intervals of time t1 ,t2 and t3. Find the ratio of ( v1 - v2) and ( v2 - v3).
t1−t2t2−t3
t1−t3t2+t3
t1+t2t2−t3
t1+t2t2+t3
The correct Answer is:D
To solve the problem, we need to find the ratio of (v1−v2) and (v2−v3) where v1,v2,v3 are the average velocities during three successive time intervals t1,t2,t3 under uniform acceleration.
1. Define Average Velocities:
- The average velocity v1 during the first interval t1 is given by:
v1=u+u12
- The average velocity v2 during the second interval t2 is:
v2=u1+u22
- The average velocity v3 during the third interval t3 is:
v3=u2+u32
2. Use Equations of Motion:
- From the equations of motion, we can express u1,u2, and u3:
- u1=u+at1
- u2=u1+at2=u+at1+at2=u+a(t1+t2)
- u3=u2+at3=u+a(t1+t2)+at3=u+a(t1+t2+t3)
3. Substitute into Average Velocities:
- Substitute u1,u2,u3 back into the expressions for v1,v2,v3:
- v1=u+(u+at1)2=2u+at12=u+at12
- v2=(u+at1)+(u+a(t1+t2))2=2u+2at1+at22=u+at1+at22
- v3=(u+a(t1+t2))+(u+a(t1+t2+t3))2=2u+2a(t1+t2)+at32=u+a(t1+t2)+at32
4. Calculate v1−v2 and v2−v3:
- Calculate v1−v2:
v1−v2=(u+at12)−(u+at1+at22)=at12−at1−at22=−at12−at22=−a(t1+t2)2
- Calculate v2−v3:
v2−v3=(u+at1+at22)−(u+a(t1+t2)+at32)=at1+at22−a(t1+t2)−at32
Simplifying gives:
=at1+at22−at1−at2−at32=−at22−at32=−a(t2+t3)2
5. Find the Ratio:
- Now we can find the ratio:
v1−v2v2−v3=−a(t1+t2)2−a(t2+t3)2=t1+t2t2+t3
Final Result:
The ratio of (v1−v2) to (v2−v3) is:
v1−v2v2−v3=t1+t2t2+t3
- The average velocity v1 during the first interval t1 is given by:
v1=u+u12
- The average velocity v2 during the second interval t2 is:
v2=u1+u22
- The average velocity v3 during the third interval t3 is:
v3=u2+u32
- From the equations of motion, we can express u1,u2, and u3:
- u1=u+at1
- u2=u1+at2=u+at1+at2=u+a(t1+t2)
- u3=u2+at3=u+a(t1+t2)+at3=u+a(t1+t2+t3)
- Substitute u1,u2,u3 back into the expressions for v1,v2,v3:
- v1=u+(u+at1)2=2u+at12=u+at12
- v2=(u+at1)+(u+a(t1+t2))2=2u+2at1+at22=u+at1+at22
- v3=(u+a(t1+t2))+(u+a(t1+t2+t3))2=2u+2a(t1+t2)+at32=u+a(t1+t2)+at32
- Calculate v1−v2:
v1−v2=(u+at12)−(u+at1+at22)=at12−at1−at22=−at12−at22=−a(t1+t2)2
- Calculate v2−v3:
v2−v3=(u+at1+at22)−(u+a(t1+t2)+at32)=at1+at22−a(t1+t2)−at32
Simplifying gives:
=at1+at22−at1−at2−at32=−at22−at32=−a(t2+t3)2
- Now we can find the ratio:
v1−v2v2−v3=−a(t1+t2)2−a(t2+t3)2=t1+t2t2+t3
The ratio of (v1−v2) to (v2−v3) is:
v1−v2v2−v3=t1+t2t2+t3
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - KINEMATIC EQUATIONS FOR UNIFORMLY ACCELERATED MOTION
32 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - RELATIVE VELOCITY
18 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - INSTANTANEOUS VELOCITY AND SPEED
16 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A particle moving with uniform acceleration has average velocities ν1,ν2 and ν3 over the successive intervals of time t1,t2 and t3 respectively. The value of ν1−ν2ν2−ν3 will be
View SolutionA particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
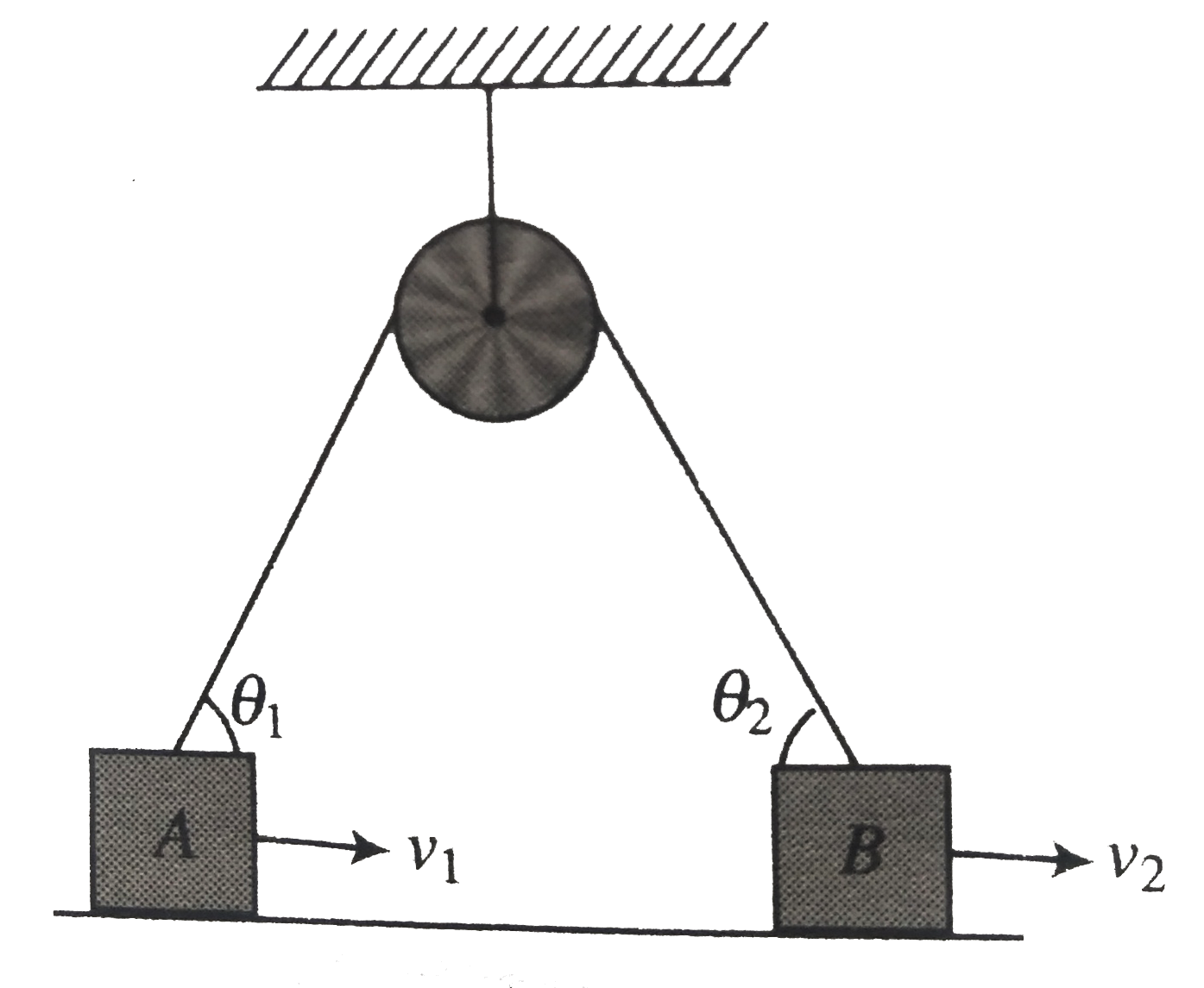
View SolutionIn fig., blocks A and B move with velocities v1 and v2 along horizontal direction. Find the ratio of v1/v2
View SolutionIf velocity of a particle is given by v=(2t+3)m/s. Then average velocity in interval 0≤t≤1 s is :
View SolutionA body moves speed V1 for distance L and then with speed V2 for distance 2L. The average speed for the motion is
View SolutionA particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
View SolutionStarting from rest a particle is first accelerated for time t1 with constant acceleration a1 and then stops in time t2 with constant retardation a2. Let v1 be the average velocity in this case and s1 the total displacement. In the second case it is accelerating for the same time t1 with constant acceleration 2a1 and come to rest with constant retardation a2 in time t3. If v2 is the average velocity in this case and s2 the total displacement, then
View SolutionStarting from rest a particle is first accelerated for time t1 with constant acceleration a1 and then stops in time t2 with constant retardation a2. Let v1 be the average velocity in this case and s1 the total displacement. In the second case it is accelerating for the same time t1 with constant acceleration 2a1 and come to rest with constant retardation a2 in time t3. If v2 is the average velocity in this case and s2 the total displacement, then
View SolutionThe ratio of de broglie wavelength of electron accelerated through potentials V1 and V2 is 1:2 the ratio of potentials V1:V2 is
View SolutionIf v1,v2andv3 are the fundamental frequencies of three segments of stretched string , then the fundamental frequency of the overall string is
View Solution
