The velocity of a particle at an instant is 10ms−1. After 3 s its velocity will becomes 16ms−1. The velocity at 2 s, before the given instant will be
6ms−1
4ms−1
2ms−1
1ms−1
The correct Answer is:A
To solve the problem step by step, we will use the first equation of motion, which relates initial velocity, final velocity, acceleration, and time.
Step 1: Identify the known values
- Initial velocity at point B (v_B) = 10 m/s (at the given instant)
- Final velocity at point C (v_C) = 16 m/s (after 3 seconds)
- Time interval (t) = 3 s
Step 2: Use the first equation of motion from point B to point C
The first equation of motion is given by:
v=u+at
Where:
- v = final velocity
- u = initial velocity
- a = acceleration
- t = time
Applying this equation from point B to point C:
vC=vB+a⋅t
Substituting the known values:
16=10+a⋅3
Step 3: Solve for acceleration (a)
Rearranging the equation to find acceleration:
16−10=a⋅3
6=3a
a=63=2m/s2
Step 4: Now, find the velocity at point A (2 seconds before point B)
We need to find the velocity at point A (v_A) which is 2 seconds before point B. We will again use the first equation of motion, this time from point A to point B.
Using the same equation:
vB=vA+a⋅t
Where:
- vB=10m/s
- a=2m/s2
- t=2s
Substituting the values:
10=vA+2⋅2
Step 5: Solve for v_A
Rearranging the equation:
10=vA+4
vA=10−4=6m/s
Final Answer
The velocity at 2 seconds before the given instant is 6 m/s.
---
- Initial velocity at point B (v_B) = 10 m/s (at the given instant)
- Final velocity at point C (v_C) = 16 m/s (after 3 seconds)
- Time interval (t) = 3 s
The first equation of motion is given by:
v=u+at
Where:
- v = final velocity
- u = initial velocity
- a = acceleration
- t = time
vC=vB+a⋅t
Substituting the known values:
16=10+a⋅3
Rearranging the equation to find acceleration:
16−10=a⋅3
6=3a
a=63=2m/s2
We need to find the velocity at point A (v_A) which is 2 seconds before point B. We will again use the first equation of motion, this time from point A to point B.
vB=vA+a⋅t
Where:
- vB=10m/s
- a=2m/s2
- t=2s
10=vA+2⋅2
Rearranging the equation:
10=vA+4
vA=10−4=6m/s
The velocity at 2 seconds before the given instant is 6 m/s.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - RELATIVE VELOCITY
18 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - HOTS
10 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ACCELERATION
19 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
The velocity of the particle at any time t is given by vu=2t(3−t)ms−1. At what time is its velocity maximum?
A2 sB3 sC2/3 sD3/2 s
The most probable velocity of a gas molecule at 298 K is 300 m/s. Its rms velocity, in m/s) is
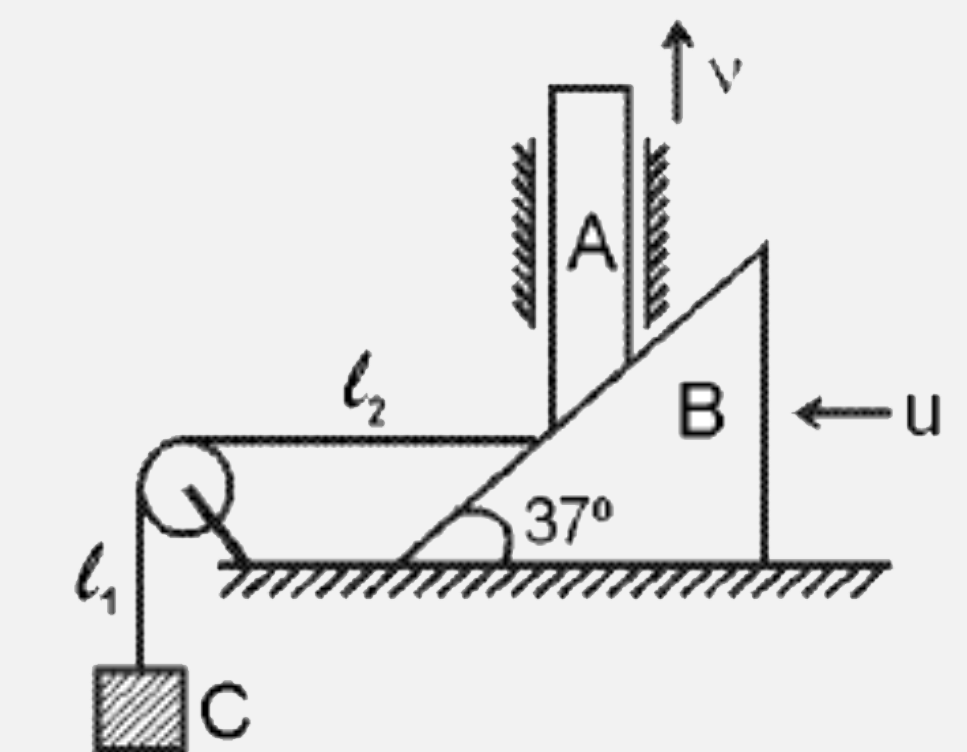
View SolutionIn the given figure , if the velocity of the block C at a particular instant is −20ms−1ˆJ , then the velocity of the rod (A) that instant will be : (string is attached to wedge )
View SolutionThe velocity of a particle moving with constant acceleration at an instant t0 is 10m/s After 5 seconds of that instant the velocity of the particle is 20m/s. The velocity at 3 second before t0 is:-
View SolutionIf the velocity of a particle is given by v=(180−16x)12ms, then its acceleration will be
View SolutionIf the velocity of a particle is given by v=(180−16x)12ms, then its acceleration will be
View SolutionIf velocity of a particle is given by v=(2t+3)m/s. Then average velocity in interval 0≤t≤1 s is :
View SolutionA particle is moving along x-axis. The position of the particle at any instant is given by x=a+bt2 where ,a= 6 m and b= 3.5 ms−2 't' is measured in second .Find
(i) the velocity of the particle at 1s and
(ii) the average velocity between 3s and 6s
View Solution