A person with outstretched arms, is spinning on a rotating stool. He suddenly brings his arms down to his sides. Which of the following is true about his kinetic energy K and angualr momentum L?
1.Both K and L increase
2.Both K and L remain unchanged
3.K remains constant, L increases
4.K increases but L remains constant
The correct Answer is:d
To solve the problem, we need to analyze the situation of a person spinning on a rotating stool with outstretched arms and then bringing their arms down to their sides. We will examine the effects on kinetic energy (K) and angular momentum (L).
1. Understanding the Initial and Final States:
- Initially, the person has their arms outstretched, which increases their moment of inertia (I).
- When the person brings their arms down, the moment of inertia decreases.
2. Conservation of Angular Momentum:
- Angular momentum (L) is given by the formula:
L=I⋅ω
where I is the moment of inertia and ω is the angular velocity.
- Since there is no external torque acting on the system, angular momentum is conserved:
Linitial=Lfinal⟹I1⋅ω1=I2⋅ω2
- Here, I1 is the moment of inertia when arms are outstretched and I2 is the moment of inertia when arms are down. Since I1>I2, it follows that ω2>ω1.
3. Analyzing Kinetic Energy:
- The rotational kinetic energy (K) is given by:
K=12Iω2
- Initially, the kinetic energy is:
K1=12I1ω21
- After the person brings their arms down, the kinetic energy becomes:
K2=12I2ω22
- Since ω2>ω1 and I2<I1, we need to analyze how these changes affect kinetic energy.
4. Comparing Kinetic Energies:
- We know that I1⋅ω1=I2⋅ω2. Rearranging gives:
ω2=I1I2⋅ω1
- As I2<I1, I1I2>1, which means ω2 is significantly greater than ω1.
- Thus, even though I2 is smaller, the increase in ω2 leads to an increase in kinetic energy:
K2>K1
5. Conclusion:
- Angular momentum (L) remains constant because there is no external torque.
- Kinetic energy (K) increases because the increase in angular velocity outweighs the decrease in moment of inertia.
Final Answer:
- Angular Momentum (L): Constant
- Kinetic Energy (K): Increases
- Initially, the person has their arms outstretched, which increases their moment of inertia (I).
- When the person brings their arms down, the moment of inertia decreases.
- Angular momentum (L) is given by the formula:
L=I⋅ω
where I is the moment of inertia and ω is the angular velocity.
- Since there is no external torque acting on the system, angular momentum is conserved:
Linitial=Lfinal⟹I1⋅ω1=I2⋅ω2
- Here, I1 is the moment of inertia when arms are outstretched and I2 is the moment of inertia when arms are down. Since I1>I2, it follows that ω2>ω1.
- The rotational kinetic energy (K) is given by:
K=12Iω2
- Initially, the kinetic energy is:
K1=12I1ω21
- After the person brings their arms down, the kinetic energy becomes:
K2=12I2ω22
- Since ω2>ω1 and I2<I1, we need to analyze how these changes affect kinetic energy.
- We know that I1⋅ω1=I2⋅ω2. Rearranging gives:
ω2=I1I2⋅ω1
- As I2<I1, I1I2>1, which means ω2 is significantly greater than ω1.
- Thus, even though I2 is smaller, the increase in ω2 leads to an increase in kinetic energy:
K2>K1
- Angular momentum (L) remains constant because there is no external torque.
- Kinetic energy (K) increases because the increase in angular velocity outweighs the decrease in moment of inertia.
- Angular Momentum (L): Constant
- Kinetic Energy (K): Increases
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - ROLLING MOTION16videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - HOTS HIGHER ORDER THINKING SKILL8videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - DYNAMICS OF ROTATIONAL MOTION ABOUT A FIXED AXIS10videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPERSEXERCISE - All Questions150videos
PRACTICE PAPERS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason10videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Which of the following statements about kinetic energy (K.E.) is true?
View SolutionA man is sitting on a rotating stool with his arms outstretched. If suddenly he folds his arms the angular velocity of the man would
View SolutionA person entering an empty room suddenly fins a snake right in front on opening the door. Which one of the following is likely to happen in his neuro-hormonal control system
View SolutionA person entering an emty room suddenly finds a snake right in fornt on opening the door. Which one of the following is likely to happen in his neuro-hormonal control system ?
View SolutionA person entering an empty room suddenly fins a snake right in front on opening the door. Which one of the following is likely to happen in his neuro-hormonal control system
View SolutionA person is spinning with his hands outstretched at the rate of 3 rad/s.When he brings his hands close to the body,he spins at the rate of 9 rad/s.The ratio of initial rotational kinetic energy to final rotational kinetic energy of the person is
View SolutionA sphere moving with a velocity v0 on a smooth surface suddenly enters on a rough horizontal surface as shown in Fig. State which of the following statements are true or false
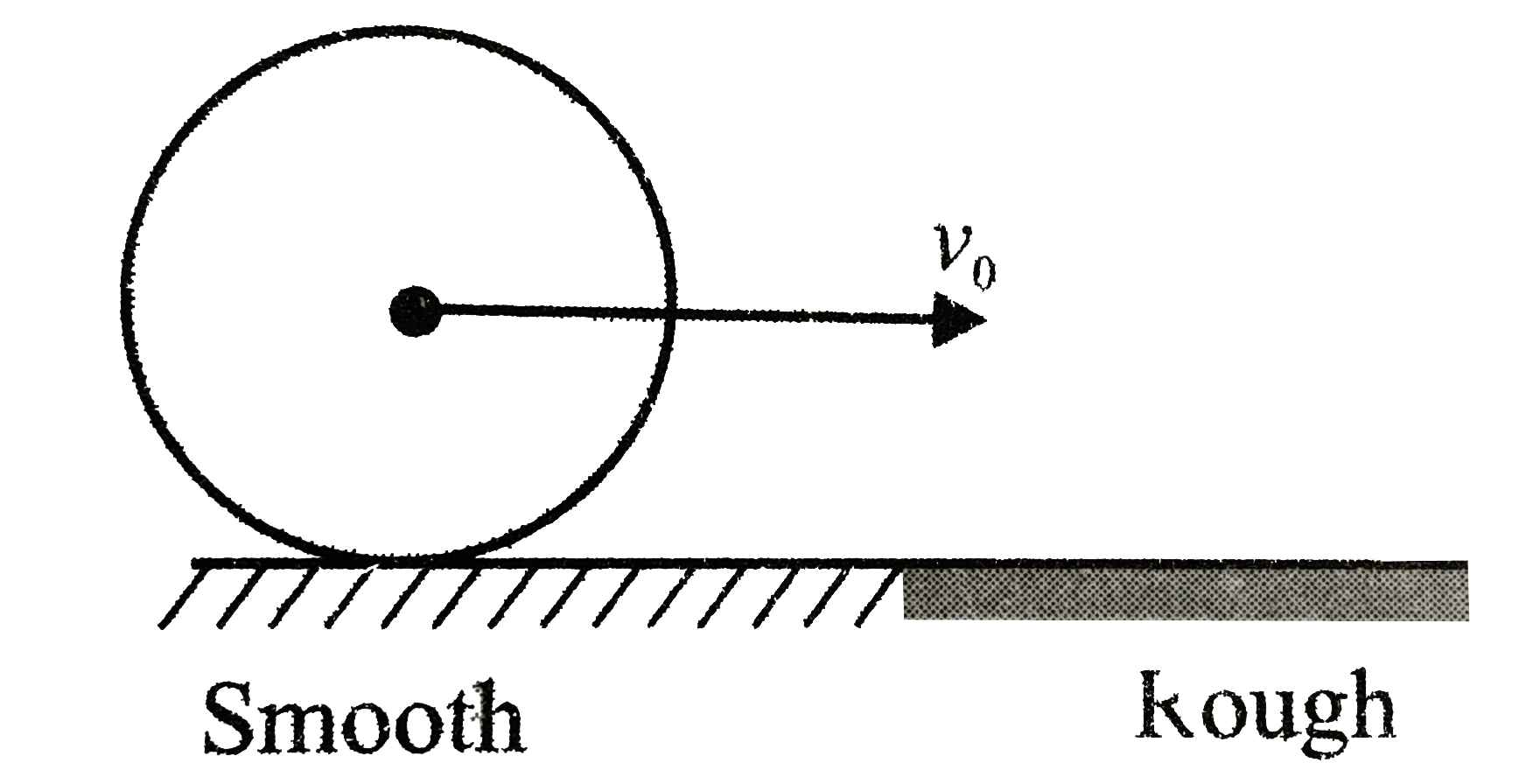
a. The sphere loses translational kinetic energy and gains rotational kinetic energy.
b. The total energy of the sphere is conserved.
c. The angular momentum of the sphere about any point OD the surface is conserved.
d. The final velocity attained by the centre of mass is 2v0/3.View SolutionLet r be the distance of a particle from a fixed point to which it is attracted by an inverse square law force given by F=k/r2 (k=constant). Let m be the mass of the particle and L be its angular momentum with respect to the fixed point. Which of the following formulae is correct about the total energy of the system?
View SolutionA young person is suffering from cancer in tongue. His tongue is completely removed, then which of the following situation will describe the person that he will be able to -
View SolutionA man spinning in free space changes the shape of his body, eg. By spreading his arms or curling up. By doing this, he can change his.
View Solution

