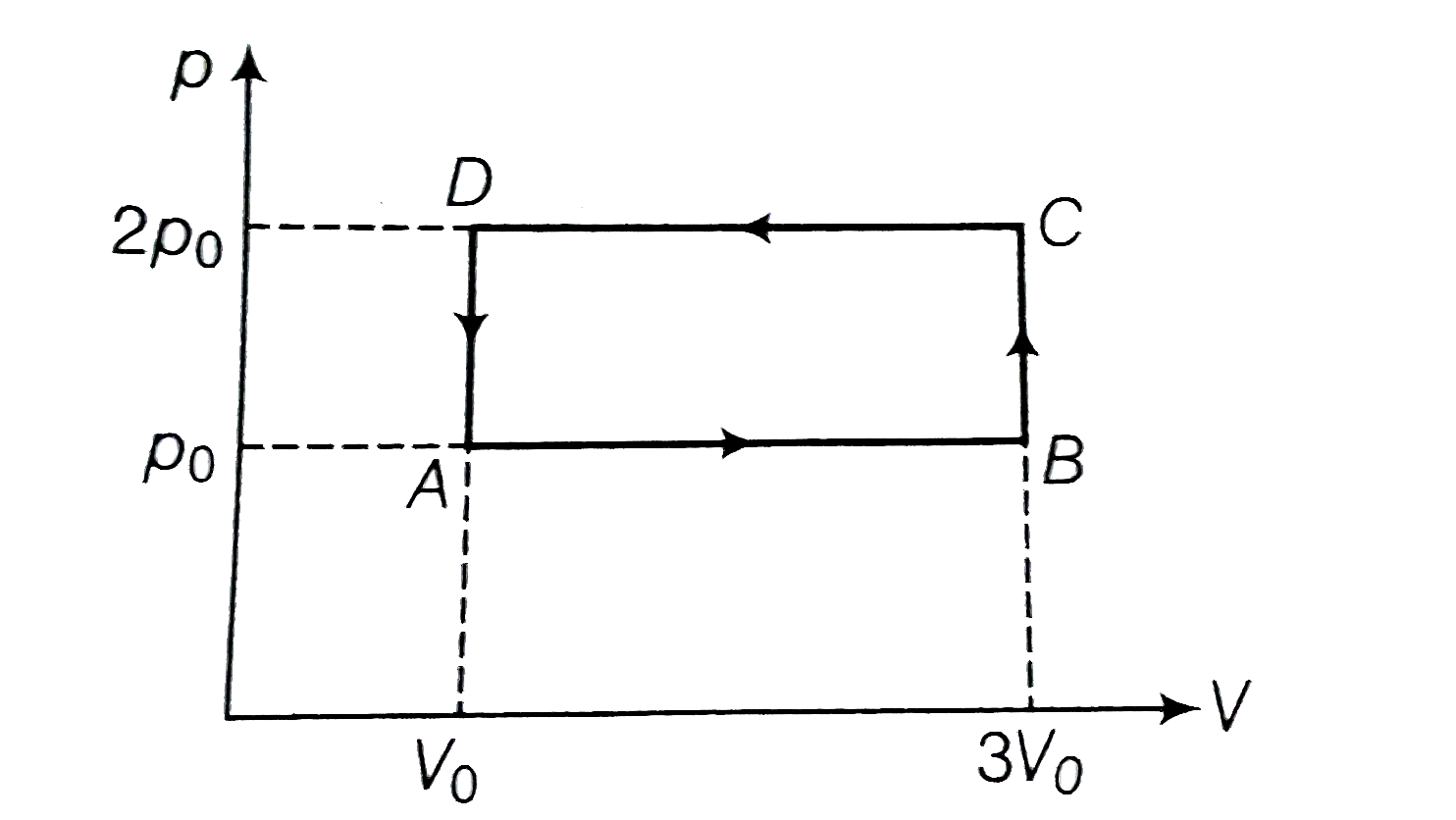
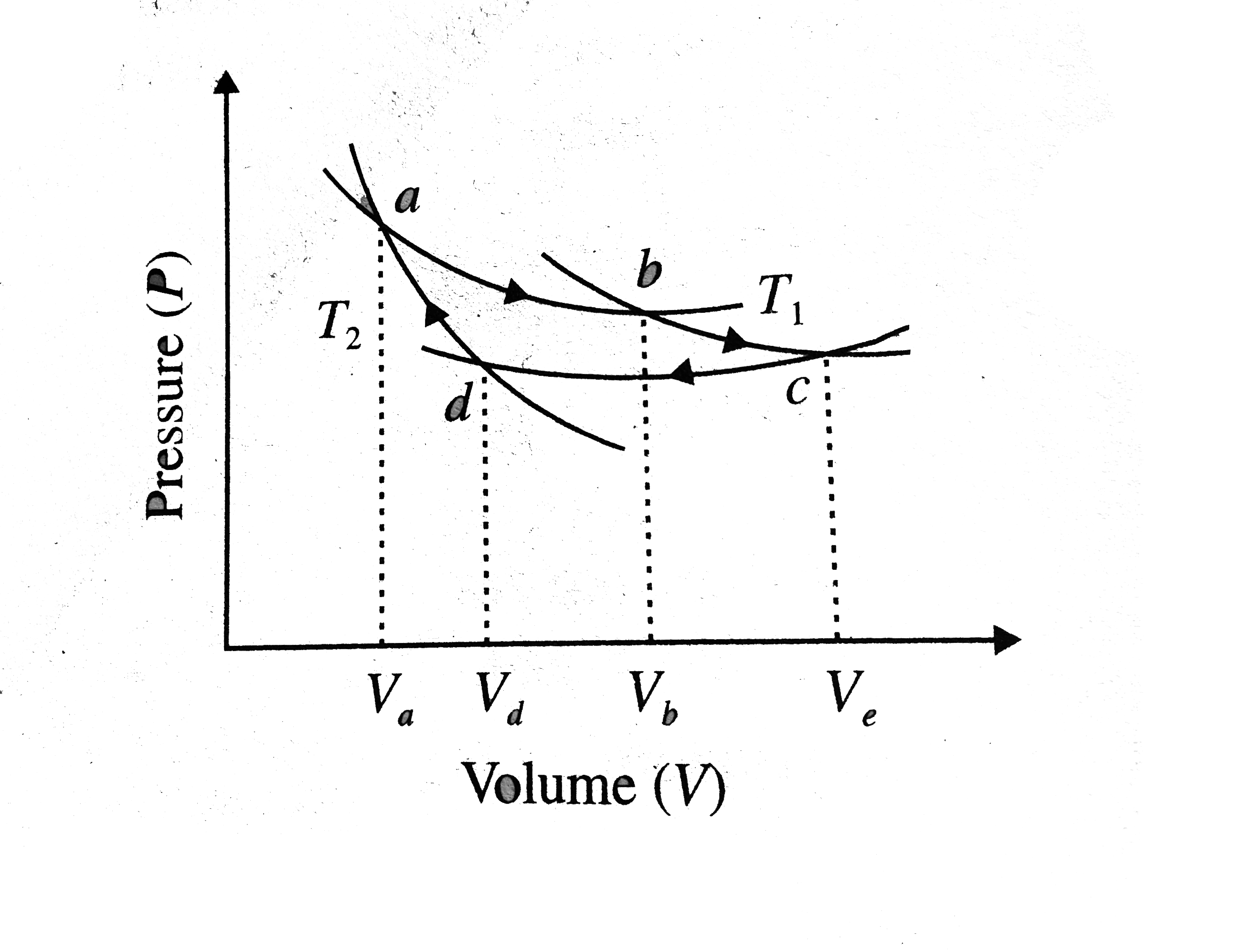One mole of an ideal gas undergoes a cyclic process ABCDA as shown in the P-V diagram, The net work done in the process is
(1 atm=10^(6) dyne cm^(-2)) 
A
500 J
B
700 J
C
800 J
D
900 J
Video Solution
Text Solution
The correct Answer is:B
As the loop is traced in clockwise direction the work done is positivbe
Work done in the process = area of rectangle aBCD
=AB×AD
Here AB=4-2=2 litre =2×103cm3
AD =8-4 = atm = 4×106dy≠cm−2
Work done , =AB×AD=2×103×4×106
=8×109rg=800J
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - HOTs8videos
THERMODYNAMICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assertion & Reason15videos
THERMODYNAMICS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason10videos
THERMAL PROPERTIES OF MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason15videos
UNITS AND MEASUREMENTS
Similar Questions
Knowledge Check
- Question 1 - Select One
An ideal gas undergoes cyclic process ABCDA as shown in given p−V diagram. The amount of work done by the gas is
 A6P0V0B−2P0V0C+2P0V0D+4P0V0
A6P0V0B−2P0V0C+2P0V0D+4P0V0 - Question 2 - Select One
A cyclic process ABCA is shown in the V−T diagram process on the P−V
 A
A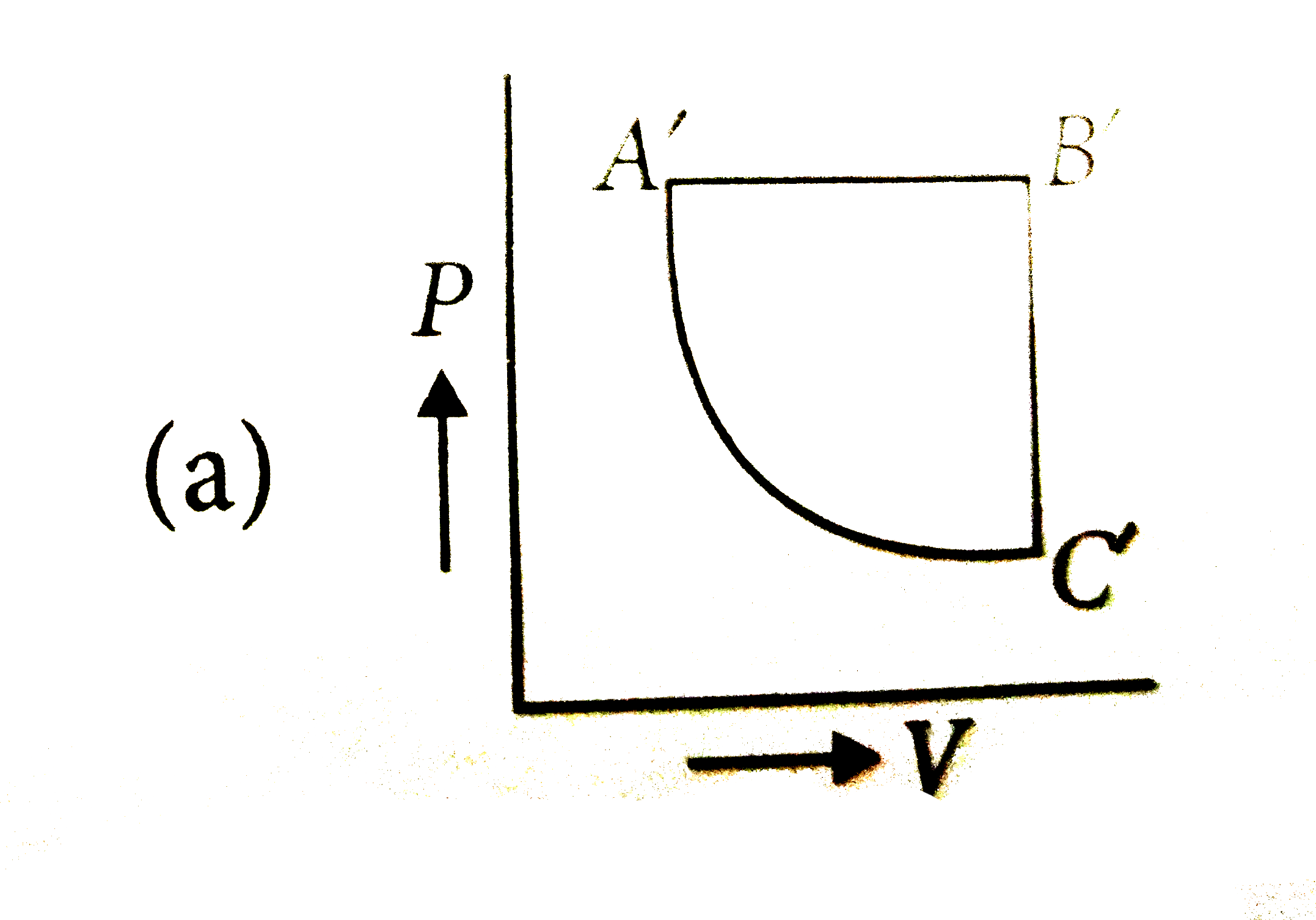 B
B C
C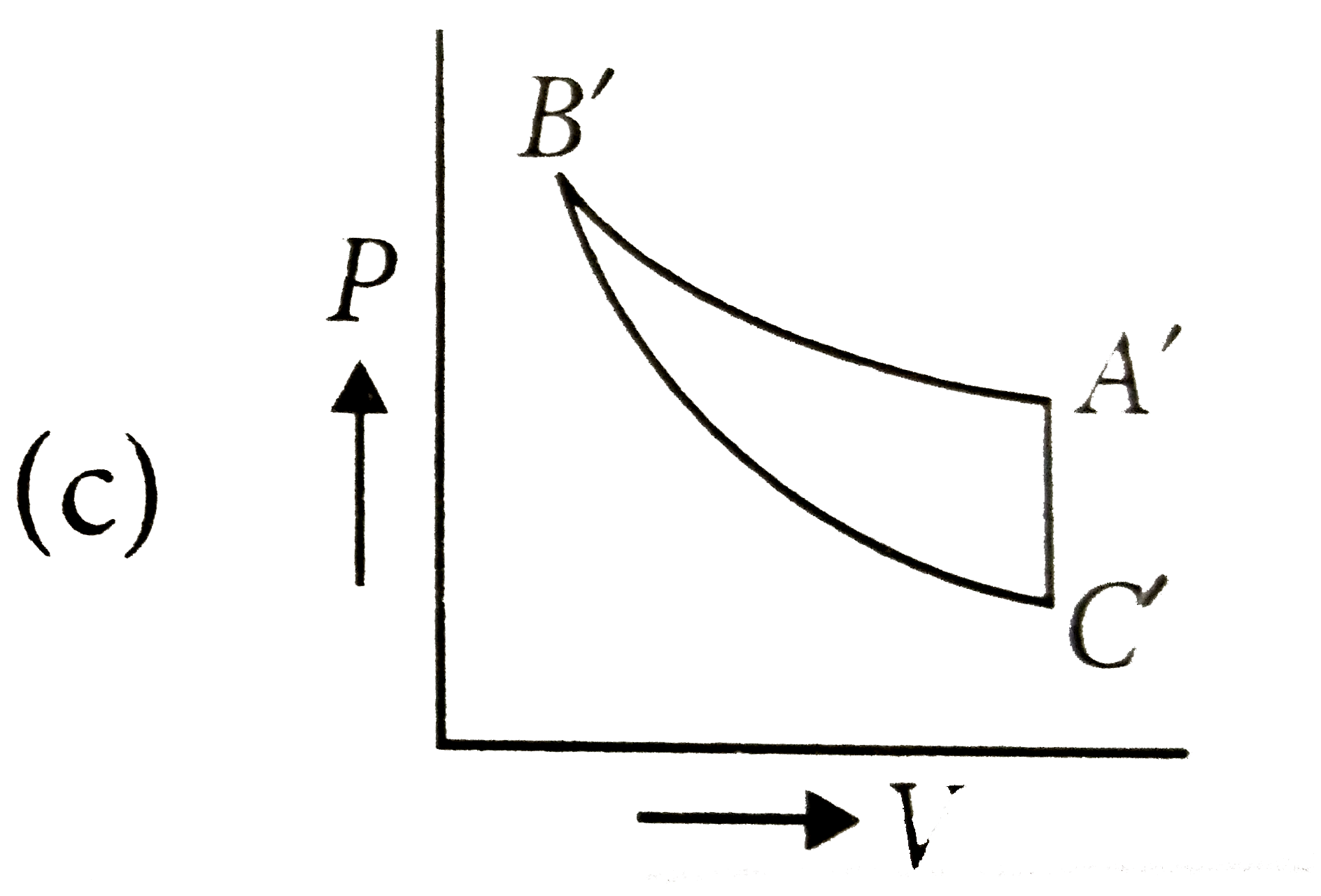 D
D
- Question 3 - Select One
A cyclic process is shown in the figure. Work done during the cyclic process ABCDA is
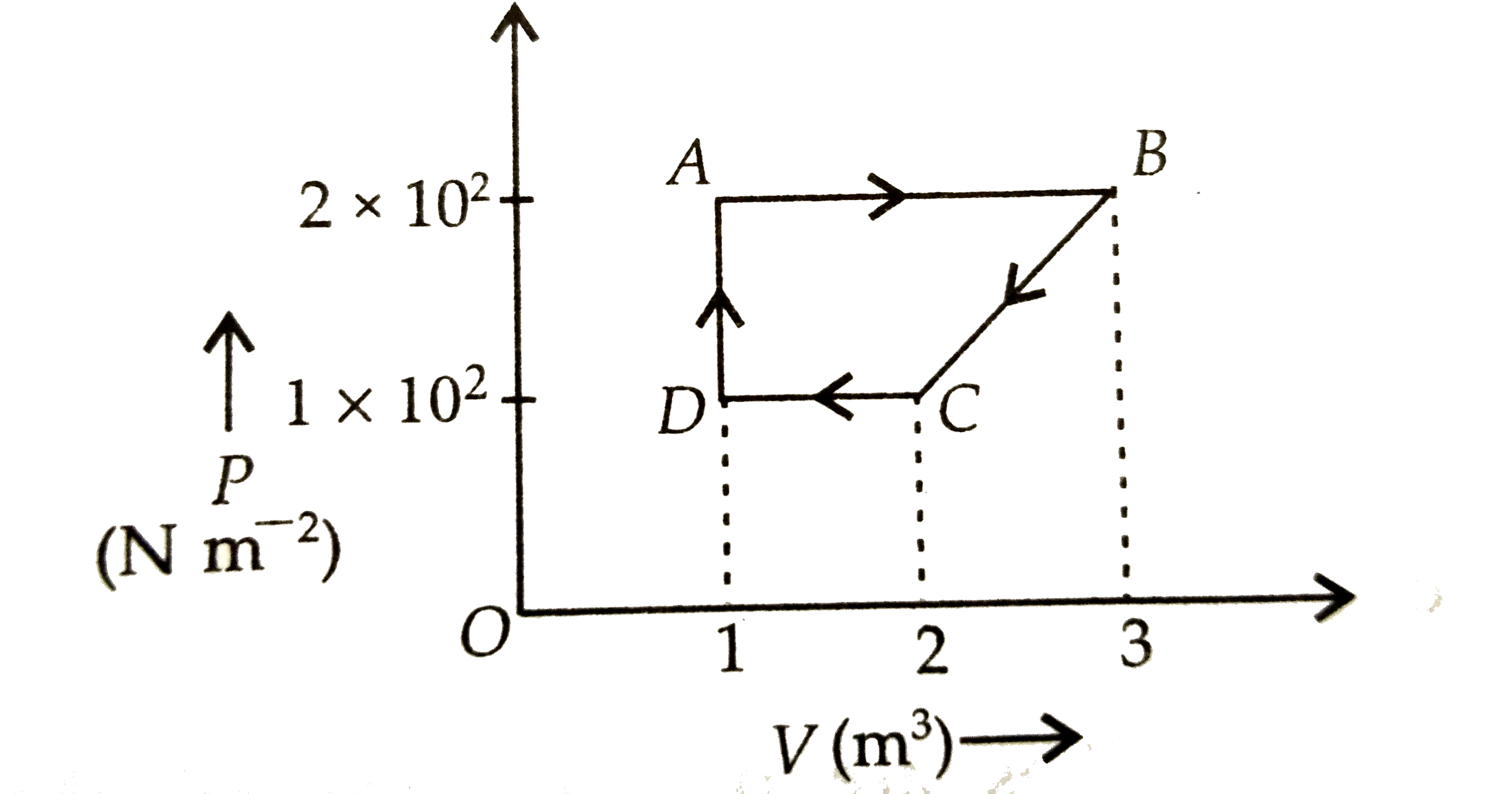 A1600 JB150 JC600 JD900 J
A1600 JB150 JC600 JD900 J
In a cyclic process shown on the P−V diargam the magnitude of the work done is :
 View Solution
View SolutionTwo moles of a monoatomic ideal gas undergoes a process AB as shown in the figure. Then, find the work done during the process in Joule.
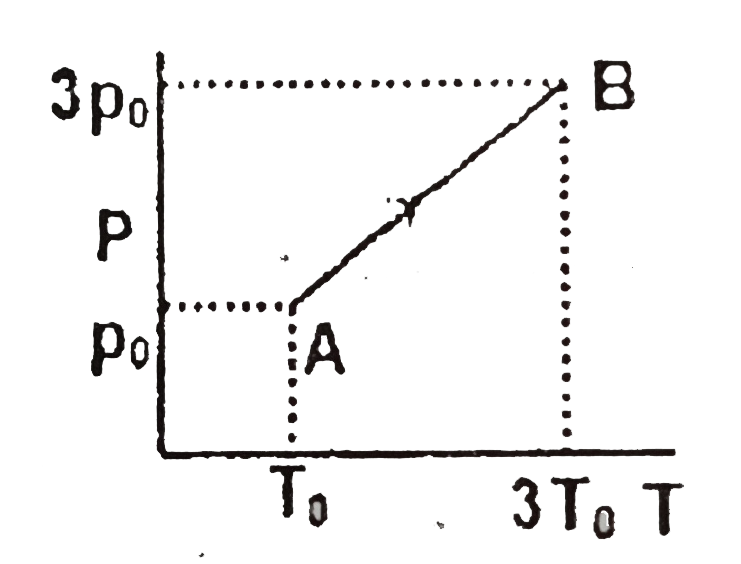 View Solution
View SolutionA thermodynamic system undergoes cyclic process ABCDA as shown in figure. The work done by the system is
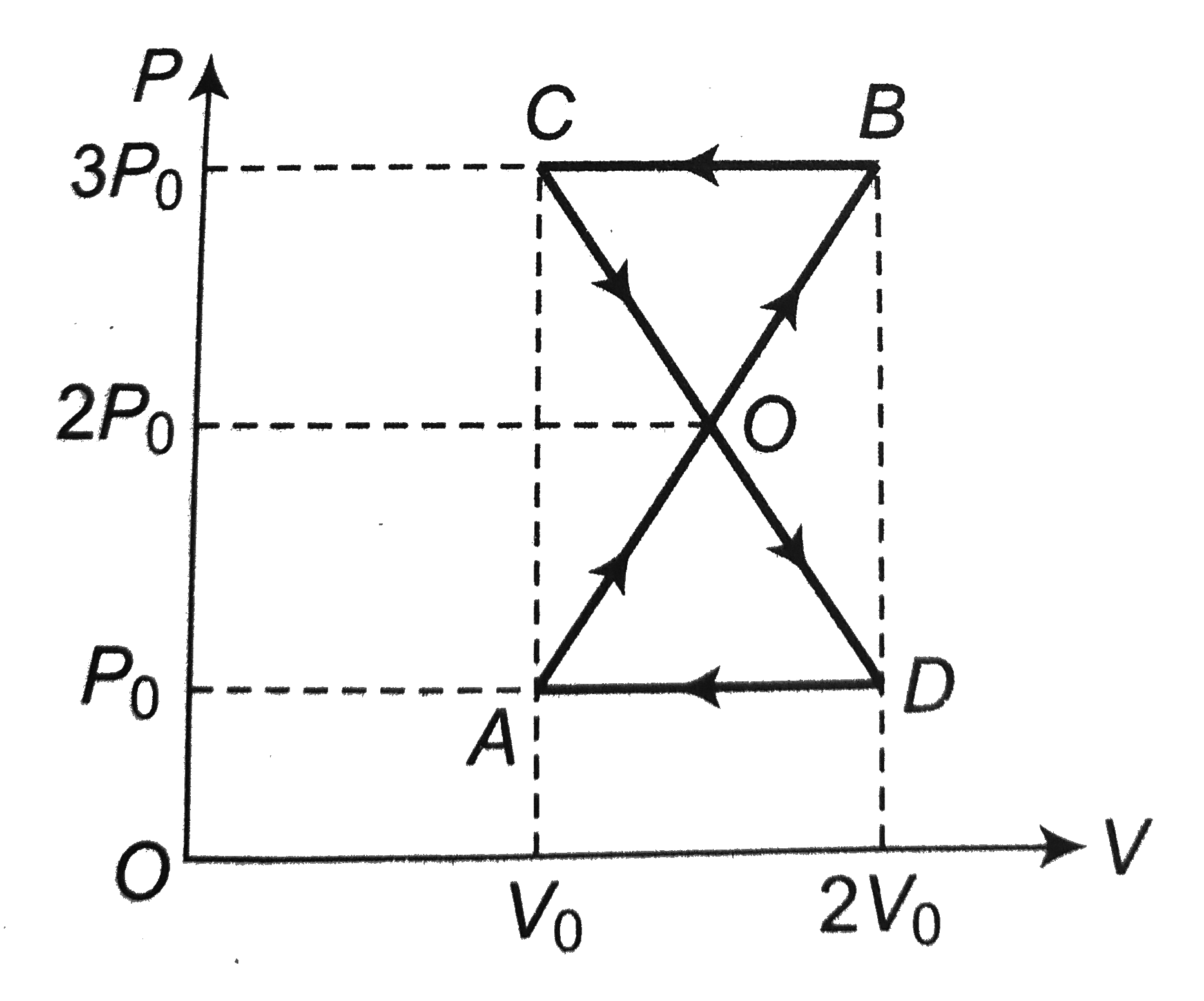 View Solution
View SolutionAn ideal gas undergoes a process P→Q→R as shown in pressure (p) - volume (v) diagram.The work done by the gas is
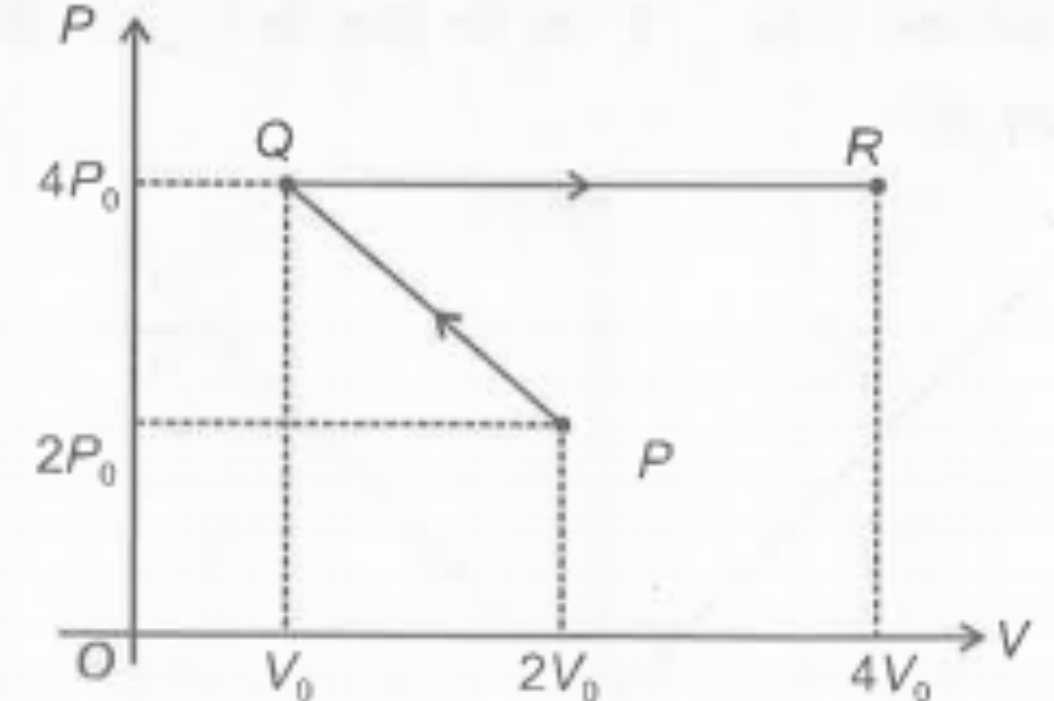 View Solution
View SolutionAn ideal gas undergoes a cyclic process as shown in the given P-T diagram, where AC is adiabatic. The process is also represented by:
 View Solution
View Solution