In a pseudo first order hydrolysis of ester in water the following result6s were obtained:
t/s0306090[Ester]0.550.310.170.085
(i) Calculate the average rate of reaction between the time interval 30 to 60 seconds.
(ii) Calculate the pseudo first order rate constant for the hydrolysis of ester.
1.91×10−2s−1
4.67×10−3molL−1s−1
1.98×10−3s−1
2.07×10−2s1
The correct Answer is:B
To solve the given problem step by step, we will break it down into two parts as indicated in the question.
Part (i): Calculate the average rate of reaction between the time interval 30 to 60 seconds.
1. Identify the concentrations at the given times:
- At t=30seconds, the concentration of ester, \((E)\) = 0.31 M
- At t=60seconds, the concentration of ester, \((E)\) = 0.17 M
2. Calculate the change in concentration:
\(
\Delta (E) = (E)_{30s} - (E)_{60s} = 0.31 - 0.17 = 0.14 \, \text{M}
\)
3. Calculate the change in time:
\(
\Delta t = 60s - 30s = 30s
\)
4. Calculate the average rate of reaction:
\(
\text{Average Rate} = \frac{\Delta (E)}{\Delta t} = \frac{0.14 \, \text{M}}{30 \, \text{s}} = 4.67 \times 10^{-3} \, \text{M/s}
\)
Part (ii): Calculate the pseudo first order rate constant for the hydrolysis of ester.
1. Use the first-order rate constant formula:
The formula for the pseudo first-order rate constant \(k\) is given by:
\(
k = \frac{2.303}{t} \log\left(\frac{(E)_0}{(E)}\right)
\)
where \((E)_0\) is the initial concentration and \((E)\) is the concentration at time \(t\).
2. Calculate \(k\) at different time intervals:
- At \(t = 30\) seconds:
\(
k_{30} = \frac{2.303}{30} \log\left(\frac{0.55}{0.31}\right)
\)
\(
k_{30} = \frac{2.303}{30} \log(1.774) \approx 1.91 \times 10^{-2} \, \text{s}^{-1}
\)
- At \(t = 60\) seconds:
\(
k_{60} = \frac{2.303}{60} \log\left(\frac{0.55}{0.17}\right)
\)
\(
k_{60} = \frac{2.303}{60} \log(3.235) \approx 1.96 \times 10^{-2} \, \text{s}^{-1}
\)
- At \(t = 90\) seconds:
\(
k_{90} = \frac{2.303}{90} \log\left(\frac{0.55}{0.085}\right)
\)
\(
k_{90} = \frac{2.303}{90} \log(6.471) \approx 2.07 \times 10^{-2} \, \text{s}^{-1}
\)
3. Calculate the average rate constant \(k\):
\(
k = \frac{k_{30} + k_{60} + k_{90}}{3} = \frac{1.91 \times 10^{-2} + 1.96 \times 10^{-2} + 2.07 \times 10^{-2}}{3}
\)
\(
k \approx 1.98 \times 10^{-2} \, \text{s}^{-1}
\)
Final Answers:
- (i) The average rate of reaction between 30 to 60 seconds is \(4.67 \times 10^{-3} \, \text{M/s}\).
- (ii) The pseudo first order rate constant for the hydrolysis of ester is \(1.98 \times 10^{-2} \, \text{s}^{-1}\).
- At t=30seconds, the concentration of ester, \((E)\) = 0.31 M
- At t=60seconds, the concentration of ester, \((E)\) = 0.17 M
\(
\Delta (E) = (E)_{30s} - (E)_{60s} = 0.31 - 0.17 = 0.14 \, \text{M}
\)
\(
\Delta t = 60s - 30s = 30s
\)
\(
\text{Average Rate} = \frac{\Delta (E)}{\Delta t} = \frac{0.14 \, \text{M}}{30 \, \text{s}} = 4.67 \times 10^{-3} \, \text{M/s}
\)
The formula for the pseudo first-order rate constant \(k\) is given by:
\(
k = \frac{2.303}{t} \log\left(\frac{(E)_0}{(E)}\right)
\)
where \((E)_0\) is the initial concentration and \((E)\) is the concentration at time \(t\).
- At \(t = 30\) seconds:
\(
k_{30} = \frac{2.303}{30} \log\left(\frac{0.55}{0.31}\right)
\)
\(
k_{30} = \frac{2.303}{30} \log(1.774) \approx 1.91 \times 10^{-2} \, \text{s}^{-1}
\)
\(
k_{60} = \frac{2.303}{60} \log\left(\frac{0.55}{0.17}\right)
\)
\(
k_{60} = \frac{2.303}{60} \log(3.235) \approx 1.96 \times 10^{-2} \, \text{s}^{-1}
\)
\(
k_{90} = \frac{2.303}{90} \log\left(\frac{0.55}{0.085}\right)
\)
\(
k_{90} = \frac{2.303}{90} \log(6.471) \approx 2.07 \times 10^{-2} \, \text{s}^{-1}
\)
\(
k = \frac{k_{30} + k_{60} + k_{90}}{3} = \frac{1.91 \times 10^{-2} + 1.96 \times 10^{-2} + 2.07 \times 10^{-2}}{3}
\)
\(
k \approx 1.98 \times 10^{-2} \, \text{s}^{-1}
\)
- (i) The average rate of reaction between 30 to 60 seconds is \(4.67 \times 10^{-3} \, \text{M/s}\).
- (ii) The pseudo first order rate constant for the hydrolysis of ester is \(1.98 \times 10^{-2} \, \text{s}^{-1}\).
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Higher Order Thinking Skills
9 Videos
- CHEMICAL KINETICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - NCERT EXEMPLAR PROBLEMS
17 Videos
- BIOMOLECULESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - BIOMOLECULESEXERCISE - Assertion And Reason
15 Videos
- CHEMISTRY IN EVERYDAY LIFE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - CHEMISTRY IN EVERYDAY LIFE EXERCISE - NCERT Exemplar
15 Videos
Similar Questions
In a pseudo first order hydrolysis of ester in water, the following results were obtained:

Calculate the pseudo first order rate constant for the hydrolysis of ester.
View SolutionIn a pseudo first order hydrolysis of ester in water, the following results were obtained:

Calculate the pseudo first order rate constant for the hydrolysis of ester.
View SolutionIn a pseudo first order hydrolysis of ester in water, the following results were obtained:

Calculate the pseudo first order rate constant for the hydrolysis of ester.
View SolutionIn a pseudo first order hydrolysis of ester in water, the following results were obtained:
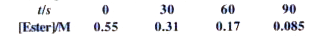
Calculate the average rate of reaction between the time interval 30 to 60 seconds.
View SolutionIn a pseudo first order hydrolysis of ester in water, the following results were obtained:
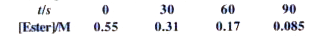
Calculate the average rate of reaction between the time interval 30 to 60 seconds.
View SolutionIn a pseudo first order hydrolysis of ester in water, the following results were obtained:
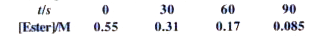
Calculate the average rate of reaction between the time interval 30 to 60 seconds.
View SolutionFor the hydrolysis of methyl acetate in aqueous solution, the following results were obtained :

(a) Show that it follows pseudo first order reaction, as the concentration of water remains constant.
(b) Calculate the average rate of reaction between the time interval 10 to 20 seconds. (Given : log 2 = 0.3010, log 4 = 0.6021)
View SolutionWhat is the concentration of the reactant in a first order reaction when the rate of the reaction is 0.6 s-1 and the rate constant is 0.035?
View SolutionAn AC source is rated 220V,50Hz. The average voltage is calculated in a time interval of 0.01s. It
View SolutionAn AC source is rated 220V,50Hz. The average voltage is calculated in a time interval of 0.01s. It
View Solution
