Match the column I with column II and mark the appropriate choice.
Column IColumn II(A)Fe(OH)3(i)Ksp=s2(B)Ag2CrO4(ii)Ksp=27s4(C)CH3COOAg(iii)Ksp=108s5(D)Ca3(PO4)(iv)Ksp=4s3
(A)→(iii),(B)→(ii),(C)→(iv),(D)→(i)
(A)→(ii),(B)→(iv),(C)→(i),(D)→(iii)
(A)→(i),(B)→(iii),(C)→(ii),(D)→(iv)
(A)→(iv),(B)→(i),(C)→(iii),(D)→(ii)
The correct Answer is:B
To solve the problem of matching Column I with Column II based on the solubility products (Ksp) of the given compounds, we will analyze each compound step-by-step.
Step 1: Analyze Fe(OH)₃
- Dissociation: Fe(OH)₃ ⇌ Fe³⁺ + 3OH⁻
- Let the solubility of Fe(OH)₃ be S.
- At equilibrium, (Fe³⁺) = S and (OH⁻) = 3S.
- Ksp Calculation:
Ksp=(Fe3+)(OH−)3=S(3S)3=S⋅27S3=27S4
- Match: Ksp = 27s⁴ (ii)
Step 2: Analyze Ag₂CrO₄
- Dissociation: Ag₂CrO₄ ⇌ 2Ag⁺ + CrO₄²⁻
- Let the solubility of Ag₂CrO₄ be S.
- At equilibrium, (Ag⁺) = 2S and (CrO₄²⁻) = S.
- Ksp Calculation:
Ksp=(Ag+)2(CrO2−4)=(2S)2(S)=4S3
- Match: Ksp = 4s³ (iv)
Step 3: Analyze CH₃COOAg
- Dissociation: CH₃COOAg ⇌ CH₃COO⁻ + Ag⁺
- Let the solubility of CH₃COOAg be S.
- At equilibrium, (CH₃COO⁻) = S and (Ag⁺) = S.
- Ksp Calculation:
Ksp=(CH3COO−)(Ag+)=S⋅S=S2
- Match: Ksp = s² (i)
Step 4: Analyze Ca₃(PO₄)₂
- Dissociation: Ca₃(PO₄)₂ ⇌ 3Ca²⁺ + 2PO₄³⁻
- Let the solubility of Ca₃(PO₄)₂ be S.
- At equilibrium, (Ca²⁺) = 3S and (PO₄³⁻) = 2S.
- Ksp Calculation:
Ksp=(Ca2+)3(PO3−4)2=(3S)3(2S)2=27S3⋅4S2=108S5
- Match: Ksp = 108s⁵ (iii)
Summary of Matches:
- A (Fe(OH)₃) matches with (ii) Ksp = 27s⁴
- B (Ag₂CrO₄) matches with (iv) Ksp = 4s³
- C (CH₃COOAg) matches with (i) Ksp = s²
- D (Ca₃(PO₄)₂) matches with (iii) Ksp = 108s⁵
Final Answer:
- A - (ii)
- B - (iv)
- C - (i)
- D - (iii)
- Dissociation: Fe(OH)₃ ⇌ Fe³⁺ + 3OH⁻
- Let the solubility of Fe(OH)₃ be S.
- At equilibrium, (Fe³⁺) = S and (OH⁻) = 3S.
- Ksp Calculation:
Ksp=(Fe3+)(OH−)3=S(3S)3=S⋅27S3=27S4
- Match: Ksp = 27s⁴ (ii)
- Dissociation: Ag₂CrO₄ ⇌ 2Ag⁺ + CrO₄²⁻
- Let the solubility of Ag₂CrO₄ be S.
- At equilibrium, (Ag⁺) = 2S and (CrO₄²⁻) = S.
- Ksp Calculation:
Ksp=(Ag+)2(CrO2−4)=(2S)2(S)=4S3
- Match: Ksp = 4s³ (iv)
- Dissociation: CH₃COOAg ⇌ CH₃COO⁻ + Ag⁺
- Let the solubility of CH₃COOAg be S.
- At equilibrium, (CH₃COO⁻) = S and (Ag⁺) = S.
- Ksp Calculation:
Ksp=(CH3COO−)(Ag+)=S⋅S=S2
- Match: Ksp = s² (i)
- Dissociation: Ca₃(PO₄)₂ ⇌ 3Ca²⁺ + 2PO₄³⁻
- Let the solubility of Ca₃(PO₄)₂ be S.
- At equilibrium, (Ca²⁺) = 3S and (PO₄³⁻) = 2S.
- Ksp Calculation:
Ksp=(Ca2+)3(PO3−4)2=(3S)3(2S)2=27S3⋅4S2=108S5
- Match: Ksp = 108s⁵ (iii)
- A (Fe(OH)₃) matches with (ii) Ksp = 27s⁴
- B (Ag₂CrO₄) matches with (iv) Ksp = 4s³
- C (CH₃COOAg) matches with (i) Ksp = s²
- D (Ca₃(PO₄)₂) matches with (iii) Ksp = 108s⁵
- A - (ii)
- B - (iv)
- C - (i)
- D - (iii)
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - EQUILIBRIUM EXERCISE - HOTS6videos
EQUILIBRIUM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - EQUILIBRIUM EXERCISE - EXEMPLAR PROBLEMS19videos
EQUILIBRIUM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ENVIRONMENTAL CHEMISTRYEXERCISE - Assertion And Reason15videos
ENVIRONMENTAL CHEMISTRY
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - HYDROCARBONS EXERCISE - Assertion And Reason15videos
HYDROCARBONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Match the column I with column II and mark the appropriate choice.
Column IColumn II(A)C2H2(i)sp3d2 hybridisation(B)SF6(ii)sp3d3 hybridisation(C)SO2(iii)sp hybridisation(D)IF7(iv)sp2 hybridisationA(A)→(i),(B)→(iii),(C)→(ii),(D)→(iv)B(A)→(iii),(B)→(i),(C)→(iv),(D)→(ii)C(A)→(ii),(B)→(iii),(C)→(i),(D)→(iv)D(A)→(iv),(B)→(i),(C)→(iii),(D)→(ii) - Question 2 - Select One
Match the compounds given in column I with oxidation states of carbon given in column II and mark the appropriate choice.
Column IColumn II(A)C6H12O6 (i) +3(B)CHCl3 (ii) -3(C)CH3CH3 (iii) +2(D)(COOH)2 (iv) 0A(A) → (iv), (B) → (iii), (C) → (ii), (D) → (i)B(A) → (i), (B) → (ii), (C) → (iii), (D) → (iv)C(A) → (ii), (B) → (iii), (C) → (iv), (D) → (i)D(A) → (iii), (B) → (ii), (C) → (i), (D) → (iv) - Question 3 - Select One
Match the column I with column II and mark the appropriate choice.
Column IColumn II(A)Borax(i)Na3AIF6(B)Inorganic benzene(ii)Na2B4O7.10H2O(C)Cryolite(iii)AI2O3.2H2O(D)Bauxite(iv)B3N3H6A(A) → (ii), (B) → (iv), (C ) → (i), (D) → (iii)B(A) → (i), (B) → (ii), (C ) → (iii), (D) → (iv)C(A) → (ii), (B) → (iii), (C ) → (i), (D) → (vi)D(A) → (iii), (B) → (i), (C ) → (ii), (D) → (iv)
Match the statement in Column I to the appropriate statement(s) from Column II.
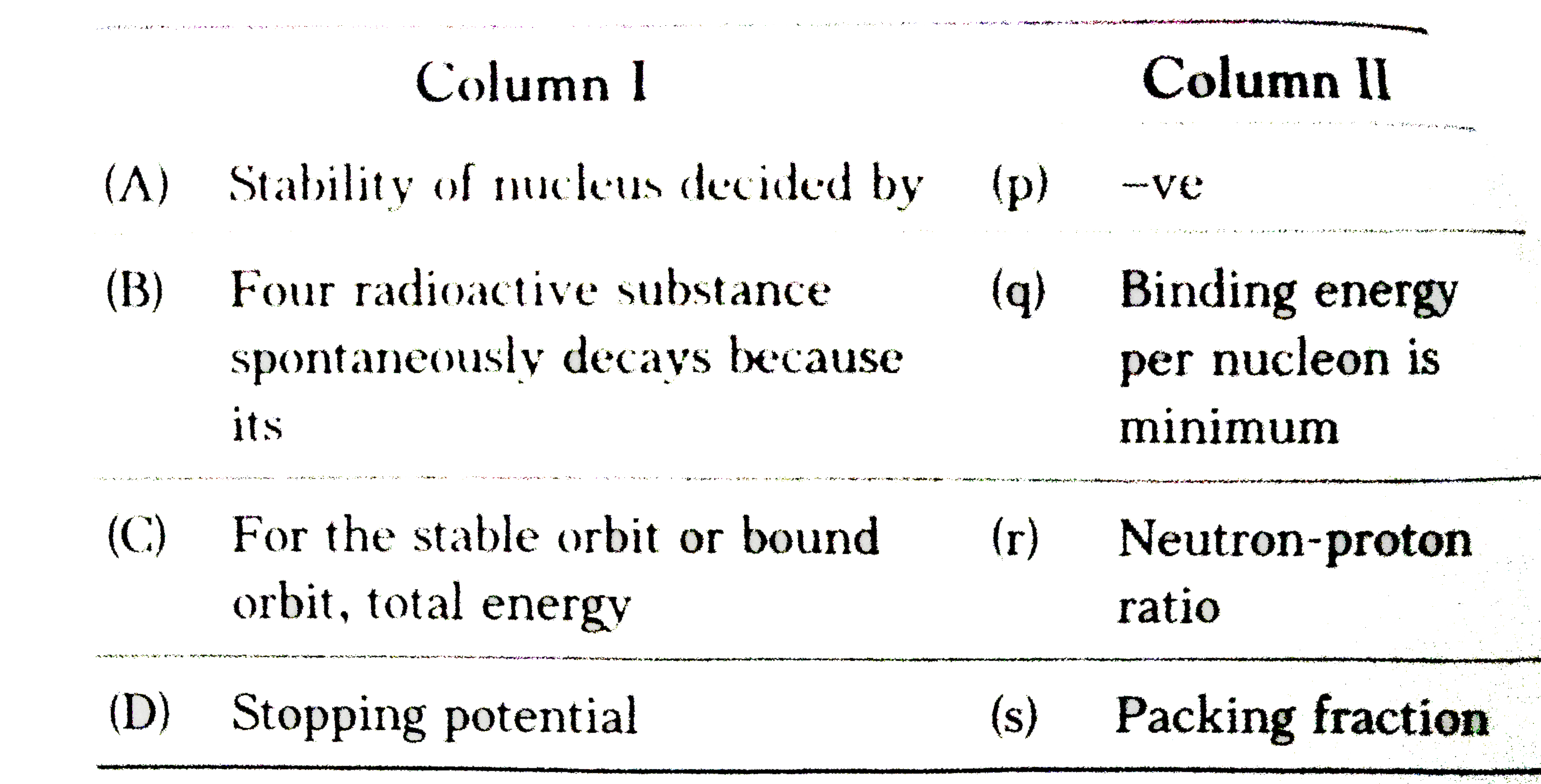 View Solution
View SolutionMatch the species in Column 1 with the type of hybrid orbitals in Column II.
Column IColumn II(a)SF4(i)sp3d2(b)lF5(ii)d2sp3(c)NO+2(iii)sp3d(d)NH+4(iv)sp3(v)spView SolutionMatch the statement in Column I to the approprate statement(s) from Column II.
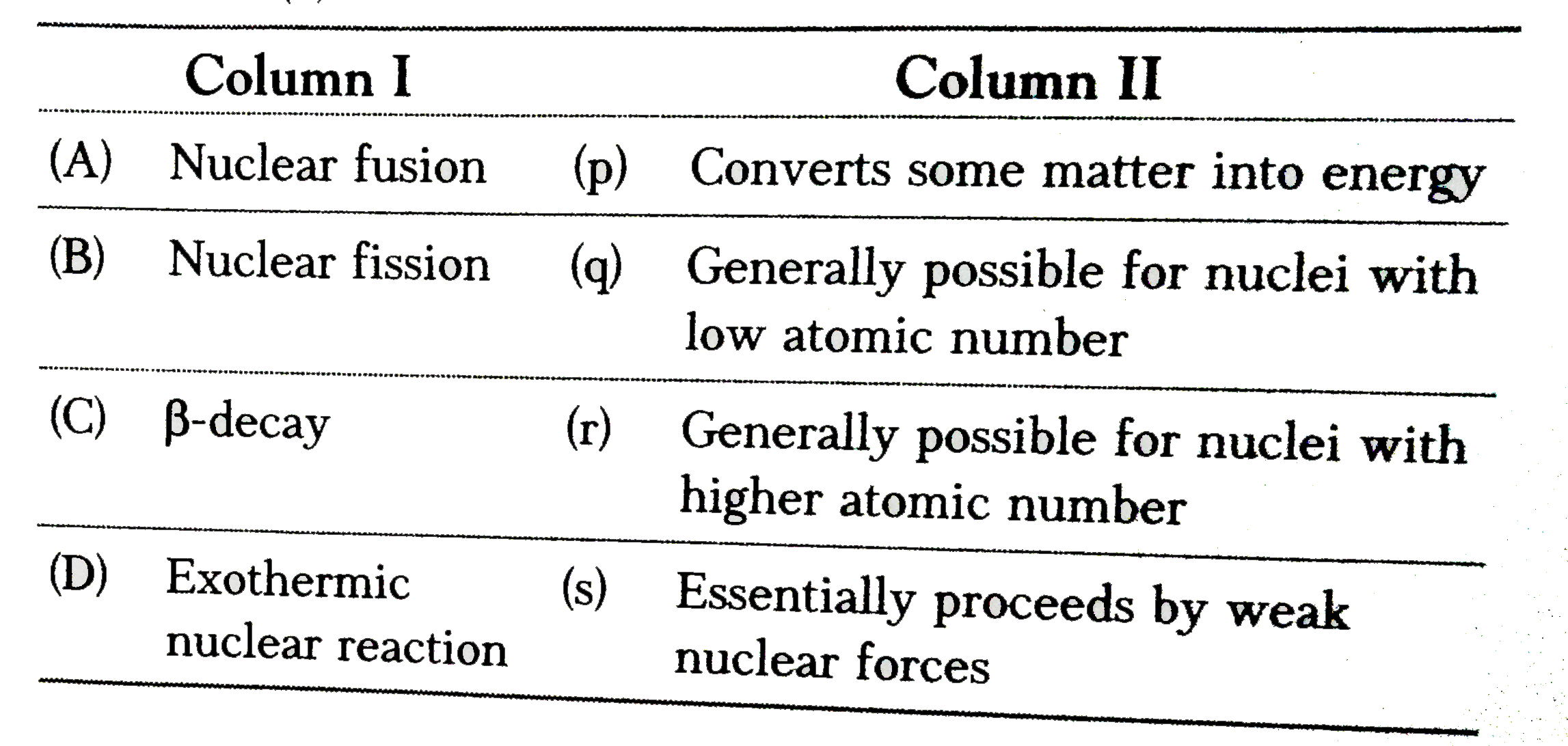 View Solution
View SolutionMatch the Column I with column II and mark the appropriate choice.
Column IColumn II(A)Coal gas(i)CO+H2(B)Synthesis gas(ii)CH4(C)Producer gas(iii)H2+CH4+CO(D)Natural gas(iv)CO+N2View SolutionMatch the rate law given in column I with the dimensions of rate constants given in column II and mark the appropriate choice.
Column IColumn II(A)Rate=k[NH3]0(i)molL−1s−1(B)Rate=k[H2O2][I−](ii)Lmol−1s−1(C)Rate=k[CH3CHO]3/2(iii)S−1(D)Rate=k[C5H5CI](iv)L1/2mol−1/2s−1View Solution


