Four resistance and are connected so that. They form the sides of a rectangle AB, BC, CD and DA respectively. Another resistance of is connected across the diagonal AC. The equivalent resistance between A and B is
A
B
C
D
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )
143 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
39 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
91 Videos
Similar Questions
Knowledge Check
Eight resistances each of resistance 5Ω are connected in the circuit as shown in figure. The equivalent resistance between A and B is
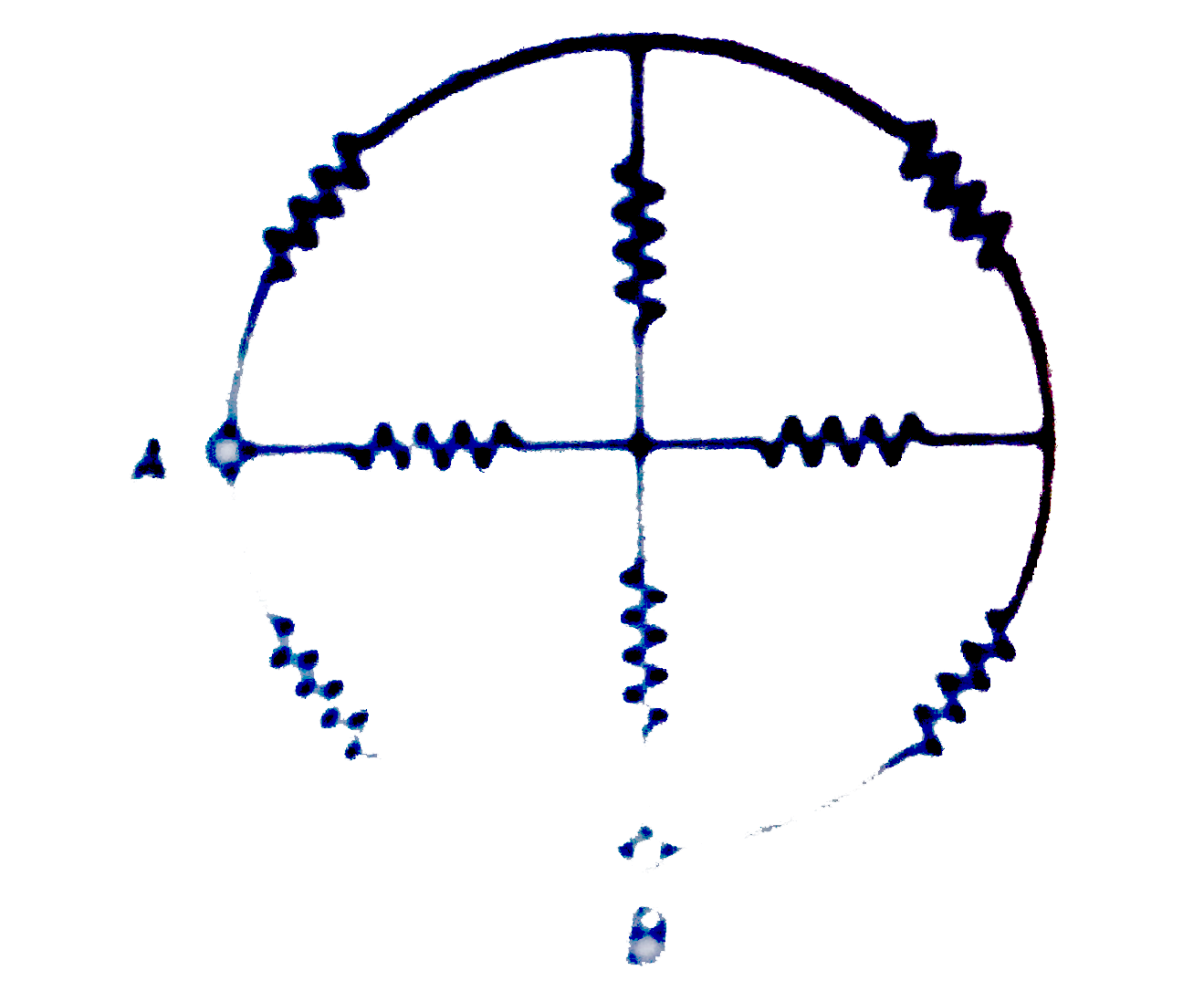 A83ΩB163ΩC157ΩD192Ω
A83ΩB163ΩC157ΩD192ΩFive 1Ω resistance are connected as shown in the figure. The resistance in the conneting wires is negligilbe. The equivalent resistance between A and B is
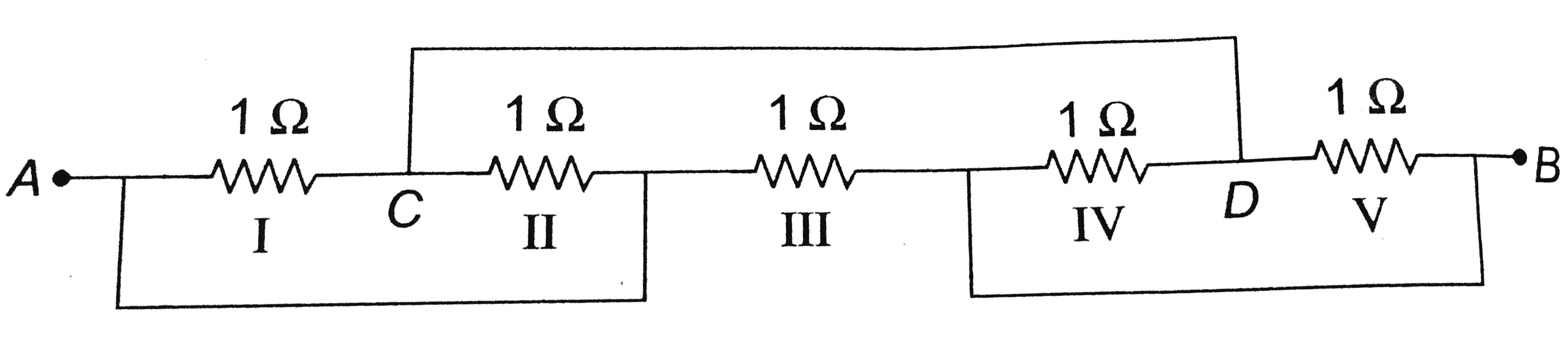 A5ΩB2.5ΩC1ΩD0.5Ω
A5ΩB2.5ΩC1ΩD0.5ΩFour resistors, 100 Ω,200Ω,300Ωand400Ω are connected to form four sides of a square. The resistors can be connected in any order. What is the maximum possible equivalent resistance across the diagonal of the square?
A210ΩB240ΩC300ΩD250Ω
Find the current through the 10Ω resistance connected across AB
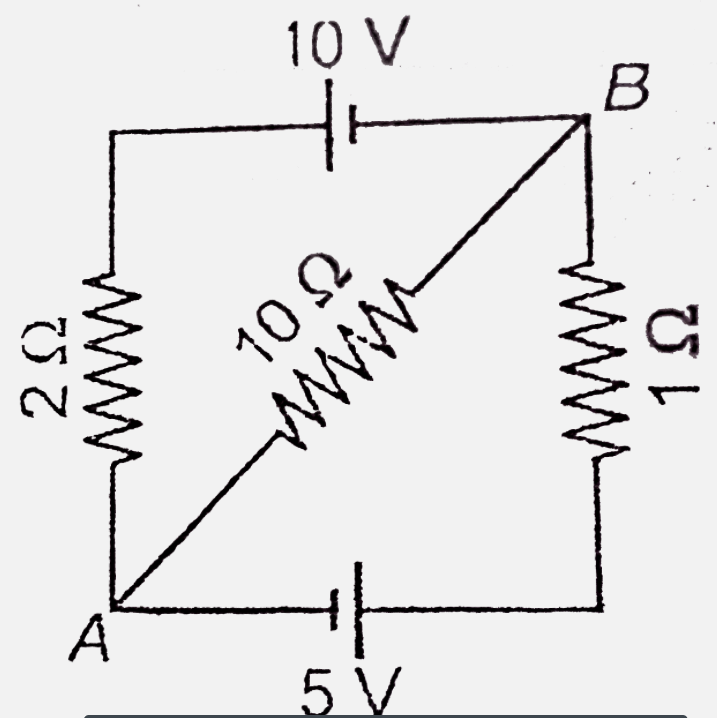
View SolutionFind the current through the 10Ω resistance connected across AB

View SolutionFour resistances of 16Ω,12Ω,4Ωand9Ω respectively are connected in cycle order so from a Wheatstone bridge. Calculate the resistance in be connected in parallel with 9Ω resistance to balance the bridge.
View SolutionTwo resistance (200±4)Ω and (150±3)Ω are connected in series . What is their equivalent resistance ?
View SolutionThe resistance of each arm of the wheat stone bridge is 10Ω. A resistance of 10Ω is connected in series with galvanometer then the equivalent resistance across the battery will be:-
View Solution
