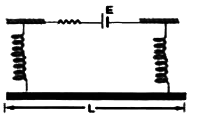
A straight rod of mass m and length L is suspended from the identical springs as shown in Fig. The spring is stretched by distance x0 due to the weight of the wire. The circuit has total resistance R0 When a magnetic field perpendicular to the plane of paper is switched on the spring are observed to extend further by the same distance. The strength of the magnetic field applied is
mgR0E
mgR0LE
mgR02LE
2mgR02LE
The correct Answer is:B
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
39 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
91 Videos
Similar Questions
A straight rod of mass m and lenth L is suspended from the identical spring as shown in the figure The spring stretched by a distance of x0 due to the weight of the wire The circuit has total resistance R When the magnetic field perpendicular to the plane of the paper is switched on, springs are observed to extend further by the same distance The magnetic field strength is

View SolutionA mass M is suspended from a light spring. An additional mass m added to it displaces the spring further by distance x then its time period is
View Solution
Knowledge Check
A straight rod of mass m and lenth L is suspended from the identical spring as shwon in the figure The spring strectched by a distance of x0 due to the weight of the wire The circuit has total resistance Rω When the magnetic field perpendicular to the plane of the paper is switched on, springs are observed to extend further by the same distance The magnetic field strenght is
 A2mgRLVBmgRLVCmgR2LVDmgRV
A2mgRLVBmgRLVCmgR2LVDmgRVA mass M is suspended from a light spring. An additional mass m added to it displaces the spring further by distance x then its time period is
AT=2π√mgx(M+m)BT=2π√(M+m)xmgCT=2π√(M+m)xMgDT=2π√MgmgThe circuit in fig. consists of wires at the top and bottom and identical metal springs at the left and right sides.The wire at the bottom has a mass of 10.0g and is 5.00cm long. The wire is hanging as shown in the figure. The springes stretch 0.500 cm under the weight of the wire, and the circuit has a total resistance of 12.0Ω. When a magnetic field is turned on the springes stretch an additional 0.300 cm.
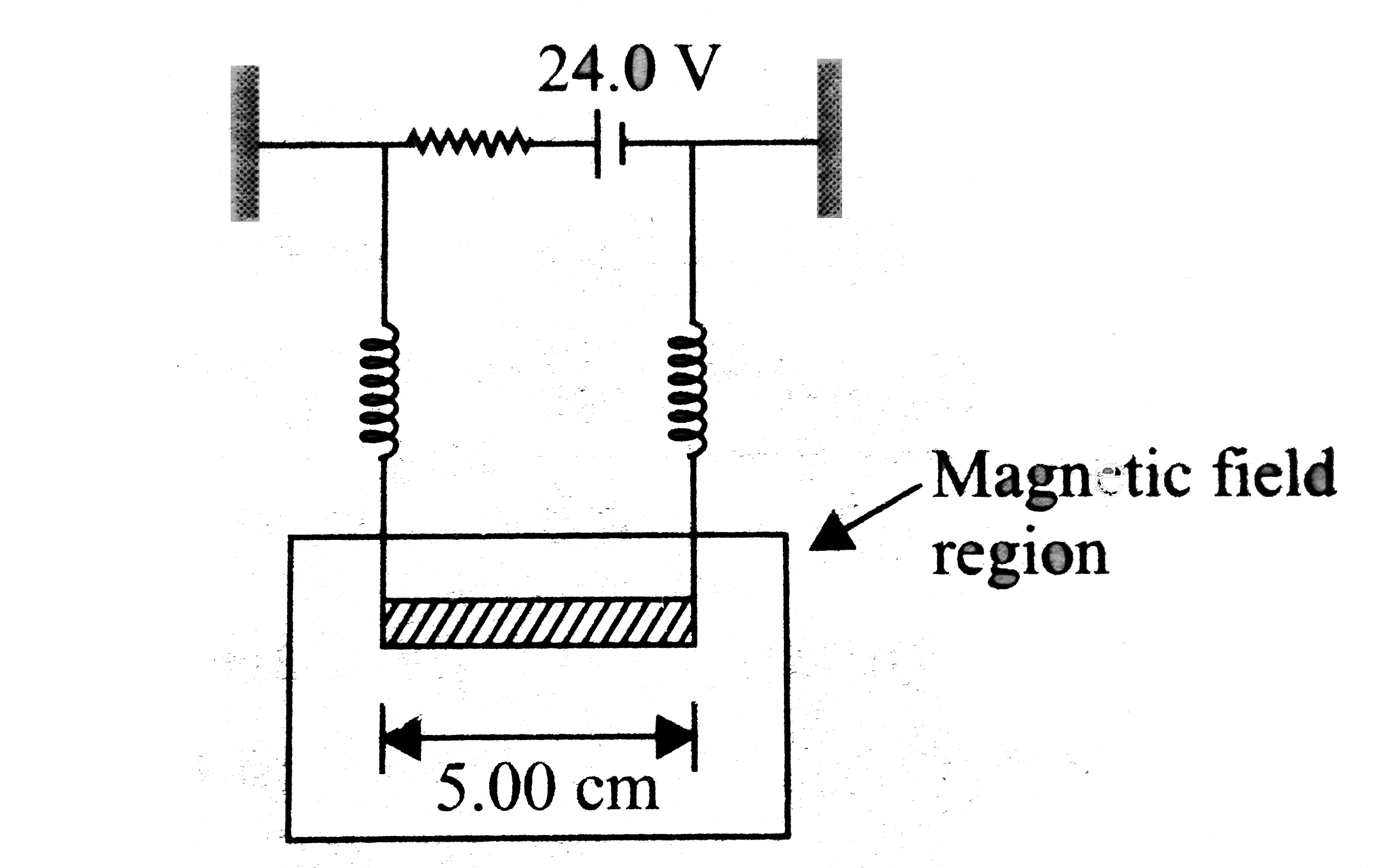
The magnitude of magnetic field isA1.2TB6TC0.6TD12T
The circuit in fig. consists of wires at the top and bottom and identical metal springs at the left and right sides.The wire at the bottom has a mass of 10.0g and is 5.00cm long. The wire is hanging as shown in the figure. The springes stretch 0.500 cm under the weight of the wire, and the circuit has a total resistance of 12.0Ω. When a magnetic field is turned on the springes stretch an additional 0.300 cm.
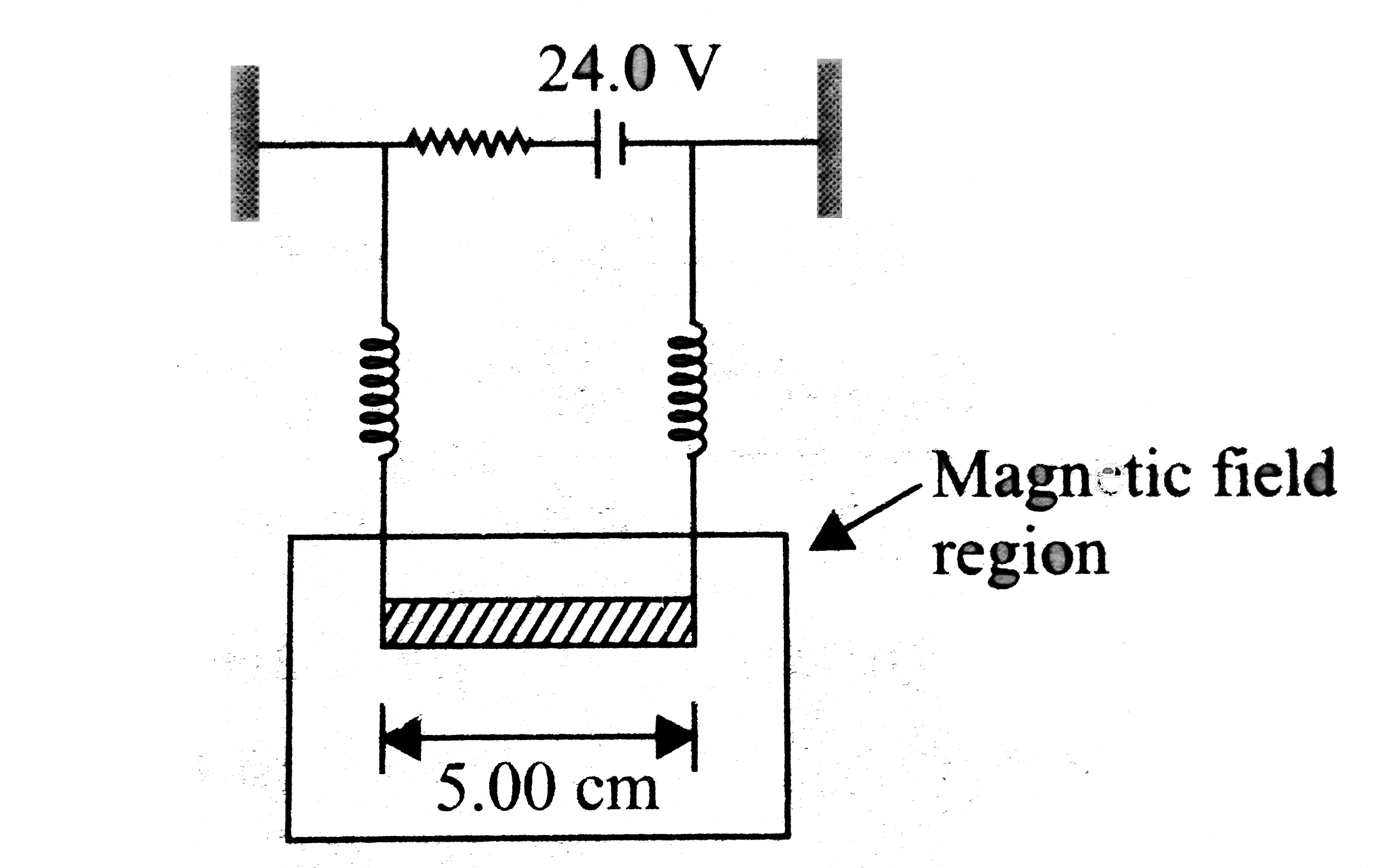
The magnitude of magnetic field is
View SolutionA metal rod of mass 10 gm and length 25 cm is suspended on two springs as shown in Fig. 1.131. The springs are extended by 4 cm. When a 20 A current passes through the rod, it rises by 1 cm. Determine the magnetic field assuming acceleration due to gravity to be 10ms−1.

View SolutionA metal rod of mass 10 gm and length 25 cm is suspended on two springs as shown in Fig. 1.131. The springs are extended by 4 cm. When a 20 A current passes through the rod, it rises by 1 cm. Determine the magnetic field assuming acceleration due to gravity to be 10ms−1.

View SolutionThe circuit in fig. consists of wires at the top and bottom and identical metal springs at the left and right sides.The wire at the bottom has a mass of 10.0g and is 5.00cm long. The wire is hanging as shown in the figure. The springes stretch 0.500 cm under the weight of the wire, and the circuit has a total resistance of 12.0Ω. When a magnetic field is turned on the springes stretch an additional 0.300 cm.
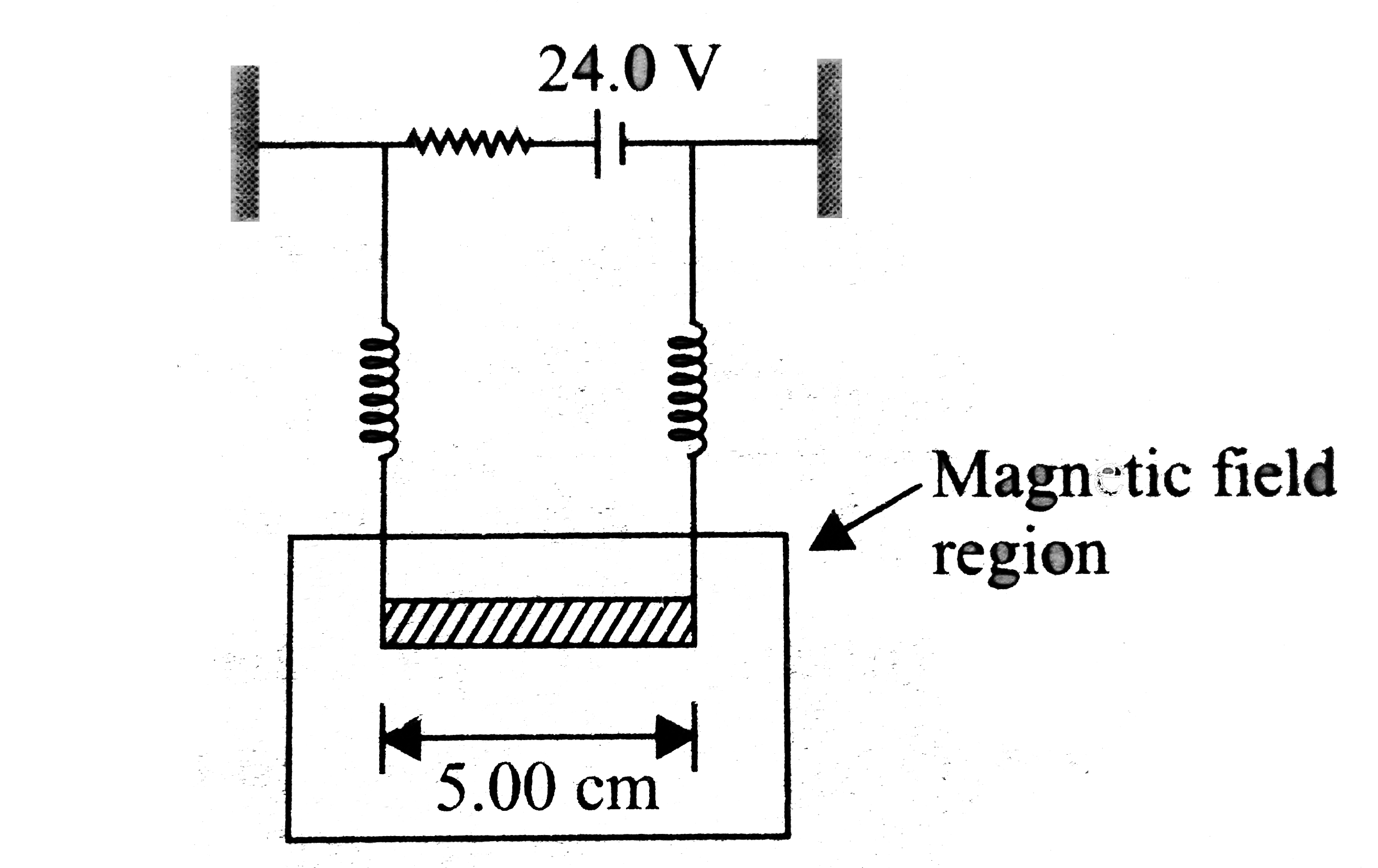
From the above statements we can conclude that
View SolutionThe circuit in fig. consists of wires at the top and bottom and identical metal springs at the left and right sides.The wire at the bottom has a mass of 10.0g and is 5.00cm long. The wire is hanging as shown in the figure. The springes stretch 0.500 cm under the weight of the wire, and the circuit has a total resistance of 12.0Ω. When a magnetic field is turned on the springes stretch an additional 0.300 cm.
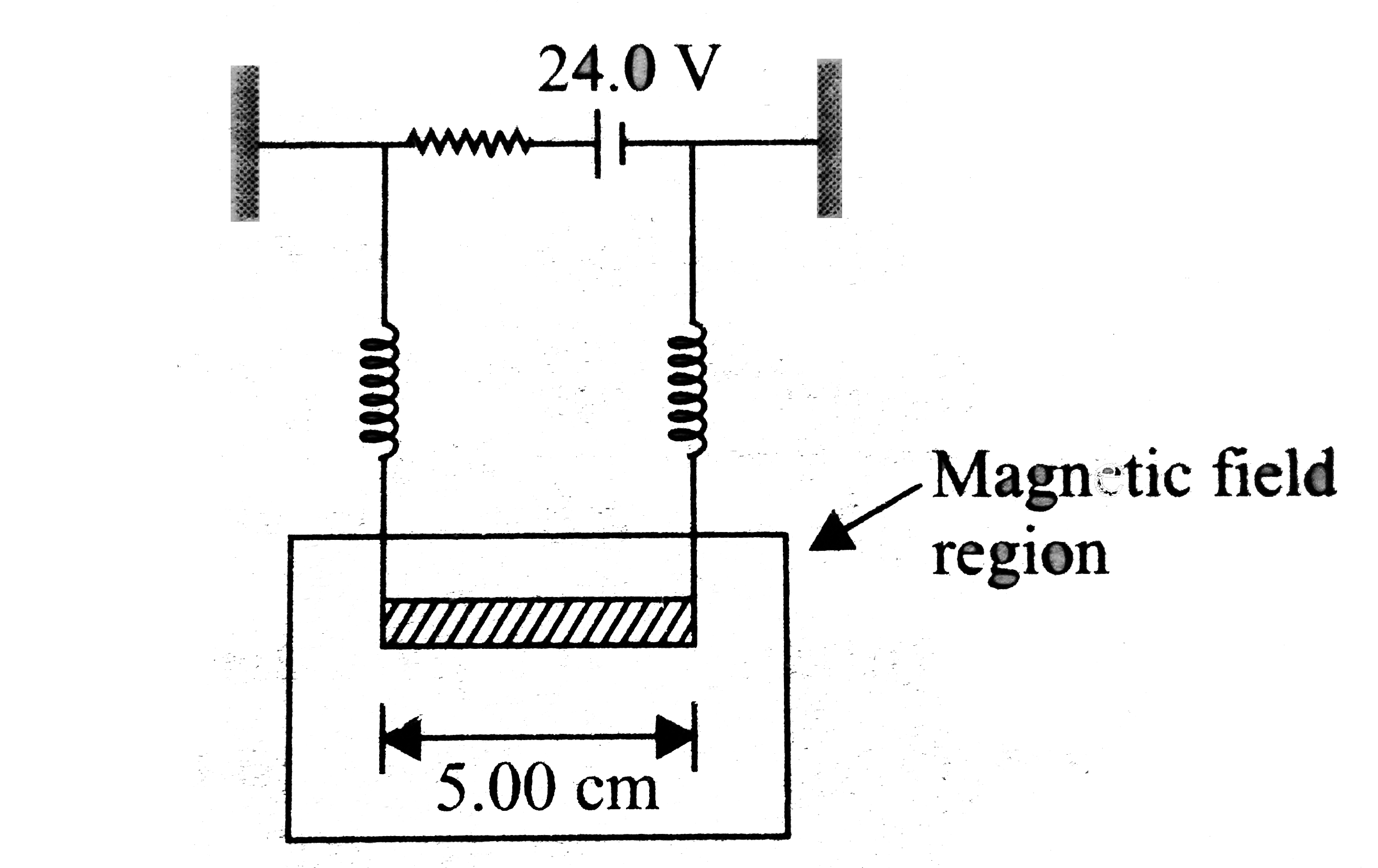
From the above statements we can conclude that
View Solution
