Several spherical drops of radius r of a liquid of surface tension T coalesce to form a single drop of radius R and volume V. The energy released in the process isnvT[1r−1R] where n = ---Solution in Telugu
The correct Answer is:3
Step by step video, text & image solution for Several spherical drops of radius r of a liquid of surface tension T coalesce to form a single drop of radius R and volume V. The energy released in the process isnvT [(1)/(r ) -(1)/(R )] where n = --- by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - LECTURE SHEET (EXERCISE-II (STRAIGHT OBJECTIVE TYPE QUESTIONS))8videos
SURFACE TENSION
- BOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - LECTURE SHEET (EXERCISE-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))2videos
SURFACE TENSION
- BOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - LECTURE SHEET (EXERCISE -I (MATRIX MATCHING TYPE QUESTIONS))1videos
SURFACE TENSION
- BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(PRACTICE SHEET (ADVANCED)) (INTEGER TYPE QUESTIONS)3videos
SIMPLE HARMONIC MOTION
- BOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE99videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A liquid rises to a height of 50 cm in a capillary tube of diameter 0.04mm. If density of liquid is 0.08×103kgm−3 angle of contact is 20°, the surface tension of the liquid is (cos20∘=0.94)
04:12View SolutionWhen a capillary tube is dipped in a liquid, the liquid rises to a height h in the tube. The free liquid surface inside the tube is hemispherical in shape. The tube is now pushed down so that the height of the tube outside the liquid is less than h. Then
01:36View SolutionMatch the following
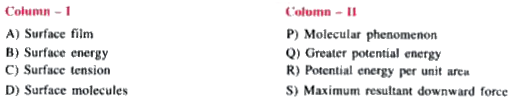 06:17View Solution
06:17View SolutionConsider the motion of a ball in a tunnel through the earth (radius of the earth is R and mass of the earth is M), the tunnel is along a chord and the ball is released from the surface. The time period of the ball is √x (approx), find x.
05:39View SolutionThe centre of mass of two particles with masses 2kg and 6 kg located at (1,1,1), (2,2,1) respectively has the coordinates
View SolutionA certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
05:39View SolutionSeveral spherical drops of a liquid of radius r coalesce to form a single drop of radius R. If T is surface tension and V is volume under consideration, then the release of energy is
View SolutionSeveral spherical drops of a liquid each of radius r coalesce to form a single drop of radius R. If T is the surface tension, then the energy liberated will be -
05:39View SolutionA certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
View SolutionA certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then:
03:45View SolutionA certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
04:14View SolutionA certain number of spherical drops of a liquid of a liquid of radius r coalesce to form a single drop of radius R and volume V. if T is the surface tension of the liquid, then
03:09View SolutionA certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
View SolutionA certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
07:02View SolutionA certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V . If T is the surface tension of the liquid, then
View Solution

