Consider a small water drop in air. If T is the surface tension, then the force due to surface tension acting on the smaller section ABC shown in the figure is 2πRTsinnθDetermine the value of n.
The correct Answer is:2
Topper's Solved these Questions
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
4 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
1 Videos
- SURFACE TENSIONBOOK - AAKASH SERIESCHAPTER - SURFACE TENSIONEXERCISE - ADDITIONAL PRACTICE EXERCISE ( LEVEL-II LECTURE SHEET (ADVANCED) MATRIX MATCHING TYPE QUESTIONS)
1 Videos
- SIMPLE HARMONIC MOTION BOOK - AAKASH SERIESCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II)(PRACTICE SHEET (ADVANCED)) (INTEGER TYPE QUESTIONS)
3 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE
99 Videos
Similar Questions
Knowledge Check
The force of surface tension on a ring situated on the surface of water is 14π×10−4 N . Then the diameter of the ring is
A5 mmB1 cmC2 cmD4 cmA water drop of radius R is split into n smaller drops , each of radius r. If T is the surface tension of water ,then the work done in the process is
A43πR3T(1r−1R)B34πR3T(1R−1r)C4πR3T(1r−1R)D6πR2(1R−1r)A drop of radius r is broken into n equal drips. Calulate the work done if surface tension of water is T.
A4rπR2nTB4rπR2T(n2/3−1)C4rπR2T(n1/3−1)DNone of the above
Consider the water drop of radius R. Find surface tension force between the left half surface and right half surface ?

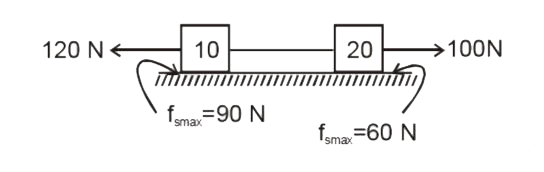
View SolutionFind the tension in the string in situation as shown in the figure below . Forces 120 N and 100N start acting when the system is at rest.
View SolutionWater is filled up to a height h in a beaker of radius R as shown in the figure. The density of water is ρ, the surface tension of water is T and the atmospheric presure is p0. Consider a vertical section ABCDof the water on one side of this section by water on the other side of this section has magnitude

(a) ∣∣2p0Rh+πR2ρgh−2RT∣∣
(b)∣∣2p0Rh+Rρgh2=2RT∣∣
(c ) ∣∣p0(π)R2+Rρgh2−2RT∣∣
(d) ∣∣p0πR2+Rρgh2+2RT∣∣.
View SolutionWater is filled up to a height h in a beaker of radius R as shown in the figure. The density of water is ρ, the surface tension of water is T and the atmospheric presure is p0. Consider a vertical section ABCDof the water on one side of this section by water on the other side of this section has magnitude

(a) ∣∣2p0Rh+πR2ρgh−2RT∣∣
(b)∣∣2p0Rh+Rρgh2=2RT∣∣
(c ) ∣∣p0(π)R2+Rρgh2−2RT∣∣
(d) ∣∣p0πR2+Rρgh2+2RT∣∣.
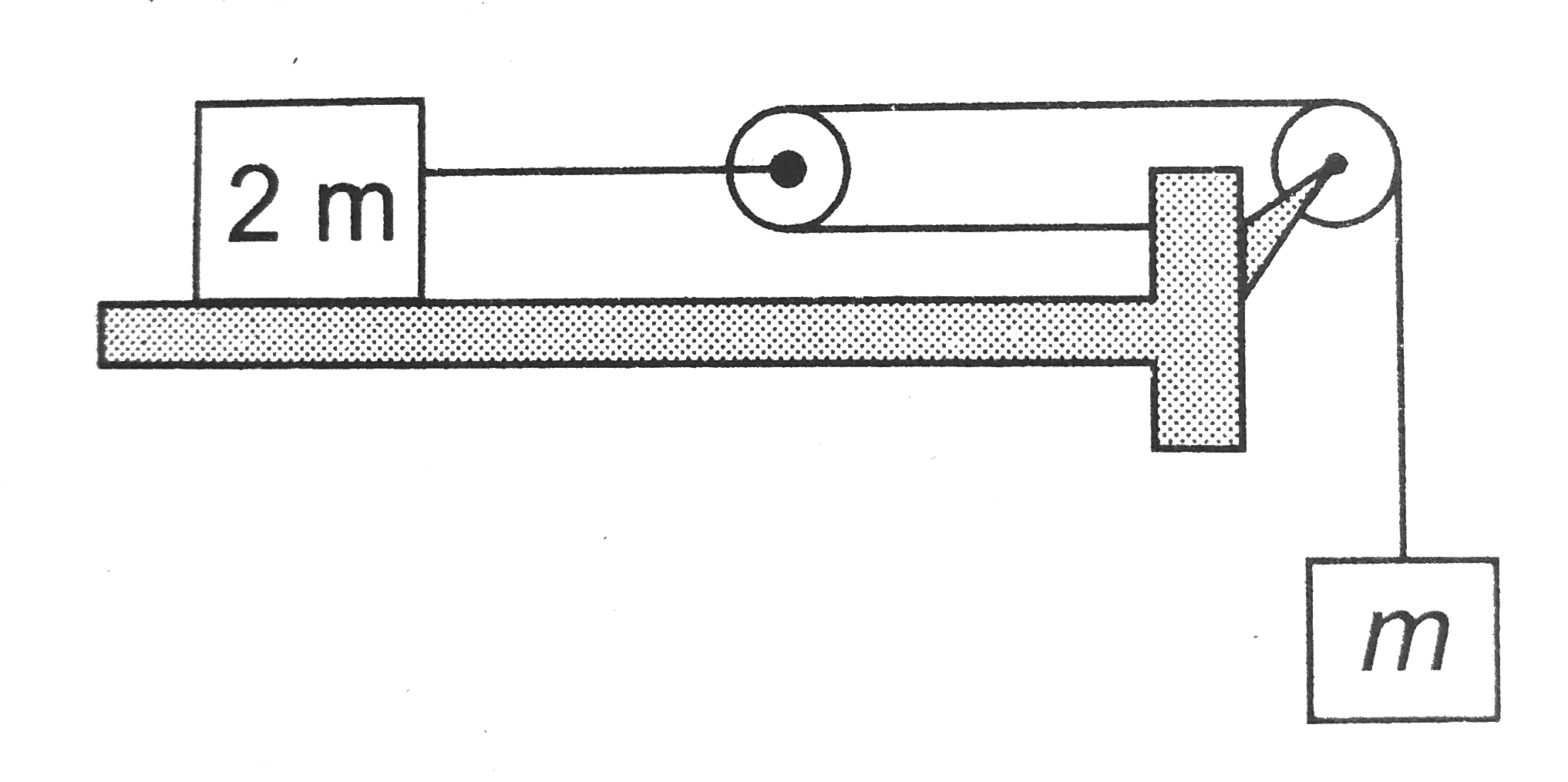
View SolutionConsider the situation shown in figure. All the surface are smooth. The tension in the string connected to 2m is.
View Solution

