A body has maximum range R1 when projected up the inclined plane. The same body when projected down the inclined plane, it has maximum range R2. Find its maximum horizontal inclined plane inte line of the greates slope.
For upward projection Rmax=v20g(1+sinβ)=R1………..i
For downward projection Rmax=v20g(1−sinβ)=R2………ii
For a projection on horizontal surface substituting β=0
Then We have Rmax=v20g=R (say) ...........iii
To establish a relation between R,R1 and R2 we need to eliminate sinβ.
Adding 1R1 from eq (i) with 1R20 from eq (ii) we have 2R=1R1+1R2
Then R=2R1R2R1+R2
Similar Questions
A body has maximum range R1 when projected up the plane. The same body when projected down the inclined plane, it has maximum range R2. Find the maximum horizontal range. Assume equal speed of projection in each case and the body is projected onto the inclined plane in the line of the greatest slope.
View SolutionA body has maximum range R1 when projected up the plane. The same body when projected down the inclined plane, it has maximum range R2. Find the maximum horizontal range. Assume equal speed of projection in each case and the body is projected onto the inclined plane in the line of the greatest slope.
View Solution
Knowledge Check
A body has maximum range R1 when projected up the inclined plane. The same body when projected down, the inclined plane. It has maximum range R2. Find its maximum horizontal range. Assume the equal speed of projection in each case and the body is projected onto the gretest slope.
 AR=2R1R2R1−R2BR=2R1R2R1+R2CR=R1R2R1−R2DR=4R1R2R1+R2
AR=2R1R2R1−R2BR=2R1R2R1+R2CR=R1R2R1−R2DR=4R1R2R1+R2As a body rolls down in inclined plane, it has
Aonly kinetic energyBonly potential energyCboth kinetic energy and potential energyDneither kinetic energy nor potential energyA projectile is projected on an inclined plane as shown in figure. 'D' is a point of maximum height from inclined plane then :
 AAB=BCBAB>BCCBC>ABDtime from A to D is equal to D to C
AAB=BCBAB>BCCBC>ABDtime from A to D is equal to D to C
A projectile when fired at a certain inclination has maximum rang R. Find its maximum height attained by it in terms of R .
View SolutionFind range of projectile on the inclined plane which is projected perpendicular to the incline plane with velcoity 20m/s as shwon in figure.
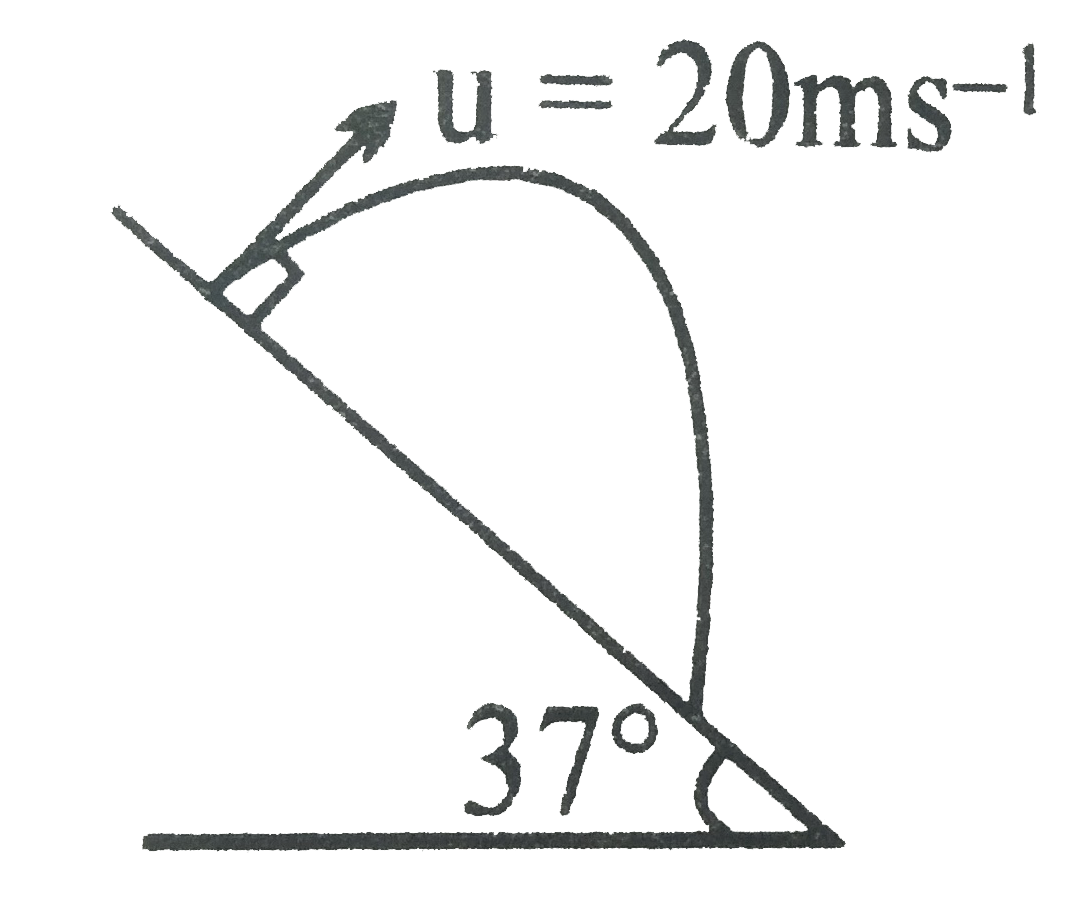
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionThe ratio of the range of the particle and its maximum range in the inclined plane is:
View SolutionIf R is the range of a projectiel on a horizontal plane and h its maximum height, the maximum horizontal range with the same velocity of projection is:
View Solution
