Two simple harmonic motions $y_{1} = A sin ω t and y_{2} = A cos ω t$ are superimposed on a particle of mass m. Find the total mechanical energy of the particle.

Text Solution

Verified by Experts

Phase difference between the two SHMs is $90^{\circ}$
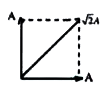
Therefore, resultant amplitude is
$A = \sqrt{2 A}, E = \frac{1}{2} m ω^{2} A_{R}^{2} = \frac{1}{2} m ω^{2} {(\sqrt{2} A)}^{2} - m ω^{2} A^{2}$

Updated on:21/07/2023

Two simple harmonic motions $y_{1} = A sin ω t$ and $y_{2}$ = Acos $ω$ t are superimposed on a particle of mass m. The total mechanical energy of the particle is
A $\frac{1}{2} m ω^{2} A^{2}$
B $m ω^{2} A^{2}$
C $\frac{1}{4} m ω^{2} A^{2}$
Dzero
Two simple harmonic motion $y_{2} A sin ω t$ and $y_{2} = A cos ω t$ are superimposed on a particle of mass $m$ . The total mechanical energy of the particle is:
A $\frac{1}{2} m ω^{2} A^{2}$
B $m ω^{2} A^{2}$
C $\frac{1}{4} m ω^{2} A^{2}$
Dzero
Two simple harmonic motions $y_{1} = A sin ω t$ and $y_{2} = A cos ω t$ are supre imposed on a particle of mass m.
A $\frac{1}{2} m ω^{2} A^{2}$
B $m ω^{2} A^{2}$
C $\frac{1}{4} m ω^{2} A^{2}$
Dzero