Two linear simple harmoic motions of equal amplitude and frequencies ω and 2ω are impressed on a particle along the axes of x and y respectively . If the initial phase difference between them is π/2 , find the resultant path followed by the particles.
We have , x= A cos ωt,y=Acos(2ωt+π/2)=−Asin2ωt
=−A(2sinωtcosωt)=−2A√1−x2A2xA=−2x√1−x2A2 or y2=6x2(1−x2A2)
Topper's Solved these Questions
- OSCILLATIONBook:AAKASH SERIESChapter:OSCILLATIONExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 31 Videos
- OSCILLATIONBook:AAKASH SERIESChapter:OSCILLATIONExercise:NUMERICAL EXERCISE (LEVEL-1)
Explore 33 Videos
- NEWTONS LAWS OF MOTION Book:AAKASH SERIESChapter:NEWTONS LAWS OF MOTION Exercise:ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANECED) (Matrix Matching Type Questions)
Explore 1 Video
- OSCILLATIONSBook:AAKASH SERIESChapter:OSCILLATIONSExercise:PRACTICE EXERCISE - SPRINGS
Explore 16 Videos
Similar Questions
Two linear harmonic motions of equal amplitudes and frequencies ω and 2 ω imposed on a particle along the axes of x and y respectively. If the initial phase difference between them is π/2, then find the resultant path followed by the particle.
View SolutionTwo linear SHM of equal amplitudes A and frequencies ω and 2ω are impressed on a particle along x and y−axes respectively. If the initial phase difference between them is π/2. Find the resultant path followed by the particle.
View Solution
Knowledge Check
Two linear simple harmonic motions of equal amplitude and frequency are impressed on a particle along x and y axis respectively. The initial phase difference between them is π2. The resultant path followed by the particle is
Aa circleBa straight lineCan ellipseDa parabolaTwo particles P and Q describe SHM of same amplitude a frequency ν along the same straight line. The maximum distance between two particles is √2a. The initial phase difference between the particles is
AzeroBπ2Cπ6Dπ3Two particles P and Q describe SHM of same amplitude a frequency ν along the same straight line. The maximum distance between two particles is √2a. The initial phase difference between the particles is
AzeroBπ2Cπ6Dπ3
Two linear SHM of equal amplitudes A and frequencies ω and 2ω are impressed on a particle along x and y−axes respectively. If the initial phase difference between them is π/2. Find the resultant path followed by the particle.
View SolutionTwo linear simple harmonic motions of equal amplitude and frequency are impressed on a particle along x and y axis respectively. The initial phase difference between them is π2. The resultant path followed by the particle is
View SolutionThe maximum seperation between two particles executing simple harmonic motion of the equal amplitude and same frequency along the same straight line and about the same mean position, is √3 times the amplitude of oscillation. IF the phase difference between them is ϕ, determine 2π/ϕ.
View SolutionTwo particles perform linear simple harmonic motion along the same path of length 2 A and period T as shown in the graph below. The phase difference between them is
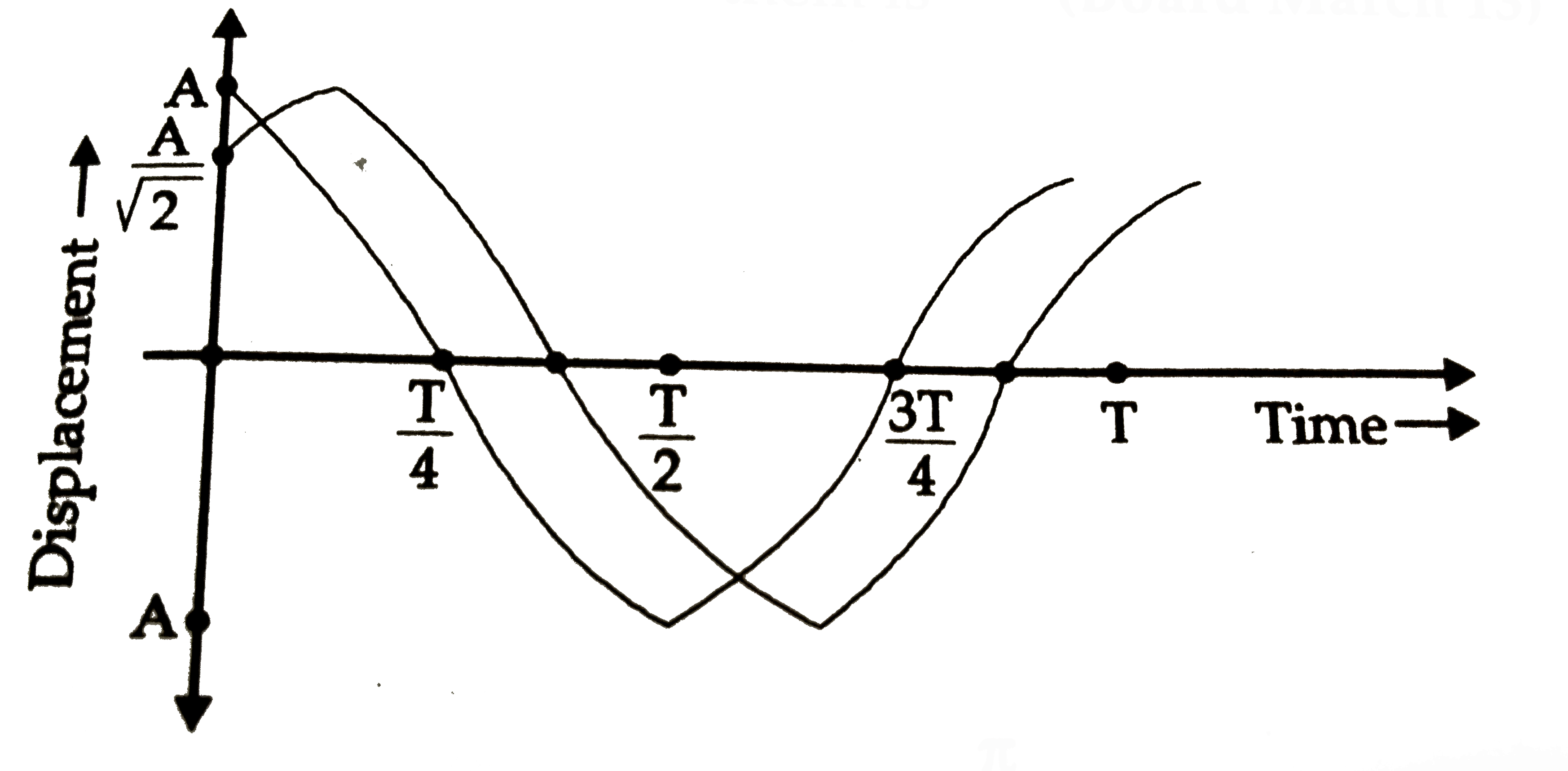
View SolutionTwo particles are executing simple harmonic of the same amplitude (A) and frequency ω along the x-axis . Their mean position is separated by distance X_(0)(X_(0)gtA). If the maximum separation between them is (X_(0)+A), the phase difference between their motion is:
View Solution
