Two moles of an ideal monatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area 4×10−3m2. The spring is, initially, in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does 50 J of work in moving the piston through a distance 0.10 m. The temperature of the gas increases by 50 K. Calculate the spring constant and the heat supplied by the heater.
W=∫PdV=∫(P0+kxA)Adx,i.e.,W=[p0Ax+12kx2]
i.e.,50=105×4×10−5×0.1×(0.1)2 then k=2000(N/m)
(b)dU=nCvdT=2×32R×50=150×8.3=1245J
But from 1st of thermodynamics : dQ =dU+dW=1245+50=1295J.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - TEST YOUR SELF
17 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - SHORT ANSWER TYPE QUESTIONS
8 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET ((ADVANCED) INTEGER/SUBJECTIVE TYPE QUESTIONS))
11 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II) PRACTICE SHEET (ADVANCED) Integer/Subjective Type Questions
2 Videos
- THERMOMETRY BOOK - AAKASH SERIESCHAPTER - THERMOMETRY EXERCISE - Numerical Exercise (LEVEL- 1)
11 Videos
Similar Questions
Two moles of an ideal monoatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area 4×10−3m2. The spring is, initially in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does 50J of work in moving the piston through a distance 0.10m. The temperature of the gas increases by 50K. Calculate the spring constant and the heat supplied by the heater. Patm=1×105N/m2R=8.314J/mol−K
View SolutionTwo moles of an ideal monoatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area 4×10−3m2. The spring is, initially in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does 50J of work in moving the piston through a distance 0.10m. The temperature of the gas increases by 50K. Calculate the spring constant and the heat supplied by the heater. Patm=1×105N/m2R=8.314J/mol−K
View Solution
Knowledge Check
Two mole of an ideal monatomic gas are confined within a cylinder by a mass less spring loaded with a frictionless piston of negligible mass and crossectional area 4×10−3m2. The gas is heated by a heater for some time. During this time the gas expands and does 50J of work in moving the piston through a distance of 0.01m. The temperature of gas increases by 50k.
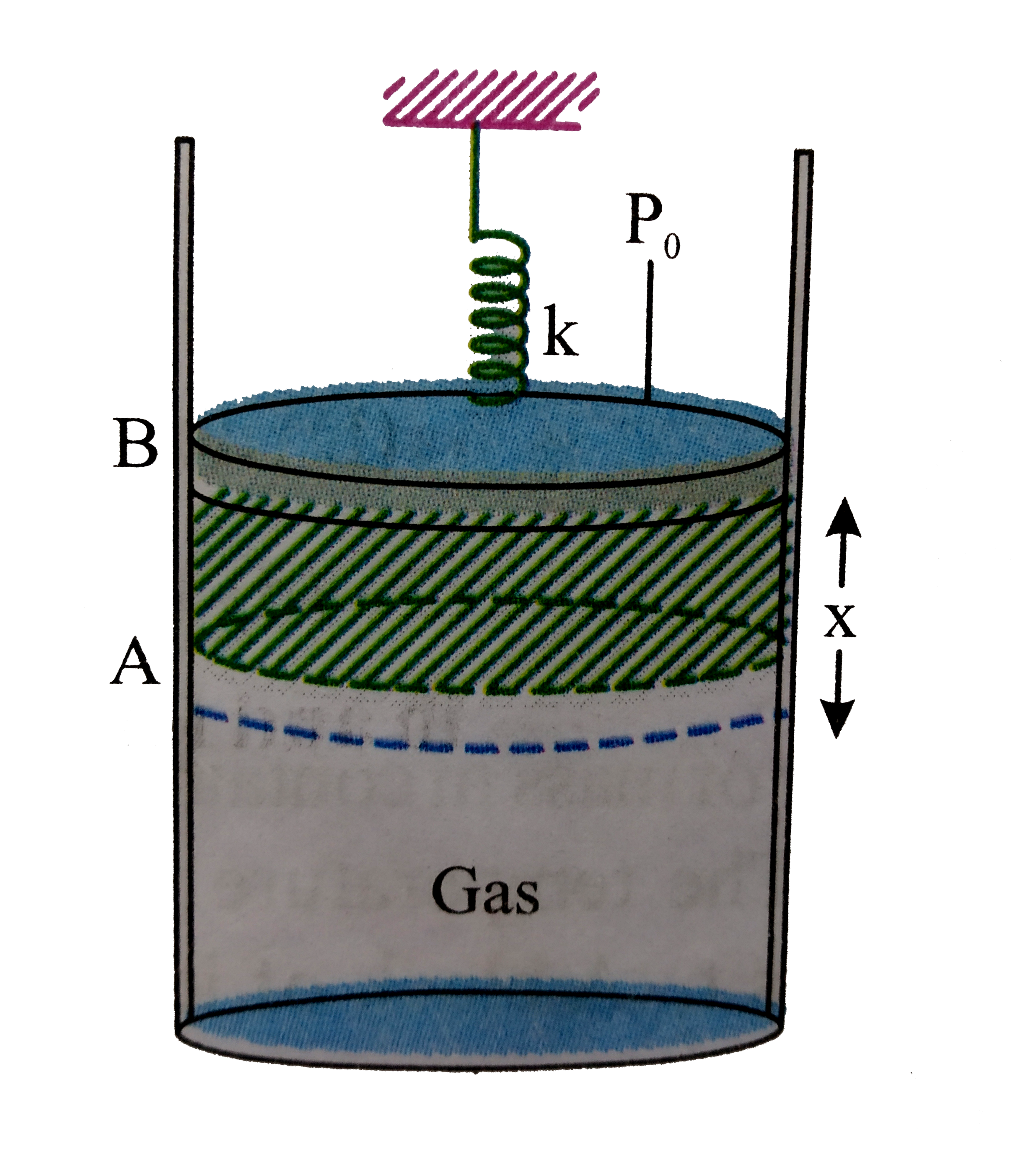
Heat supplied by heater during this process isA129.65JB1296.5JC12.96JD250JTwo mole of an ideal monatomic gas are confined within a cylinder by a mass less spring loaded with a frictionless piston of negligible mass and crossectional area 4×10−3m2. The gas is heated by a heater for some time. During this time the gas expands and does 50J of work in moving the piston through a distance of 0.01m. The temperature of gas increases by 50k.
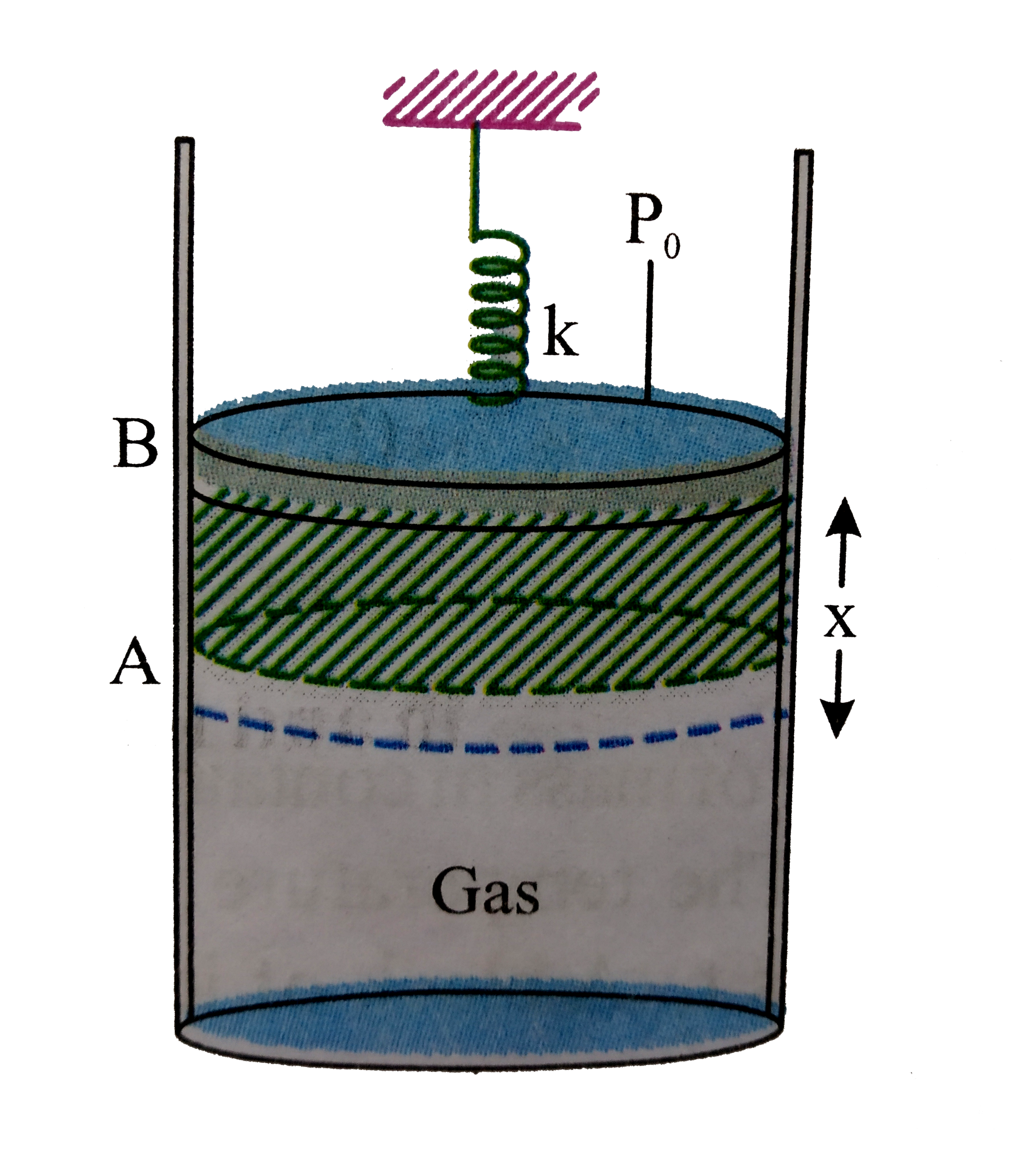
Change in internal energy of the gas isA1246.5JB124.65JC200JD12.46JTwo mole of an ideal monatomic gas are confined within a cylinder by a mass less spring loaded with a frictionless piston of negligible mass and crossectional area 4×10−3m2. The gas is heated by a heater for some time. During this time the gas expands and does 50J of work in moving the piston through a distance of 0.01m. The temperature of gas increases by 50k.
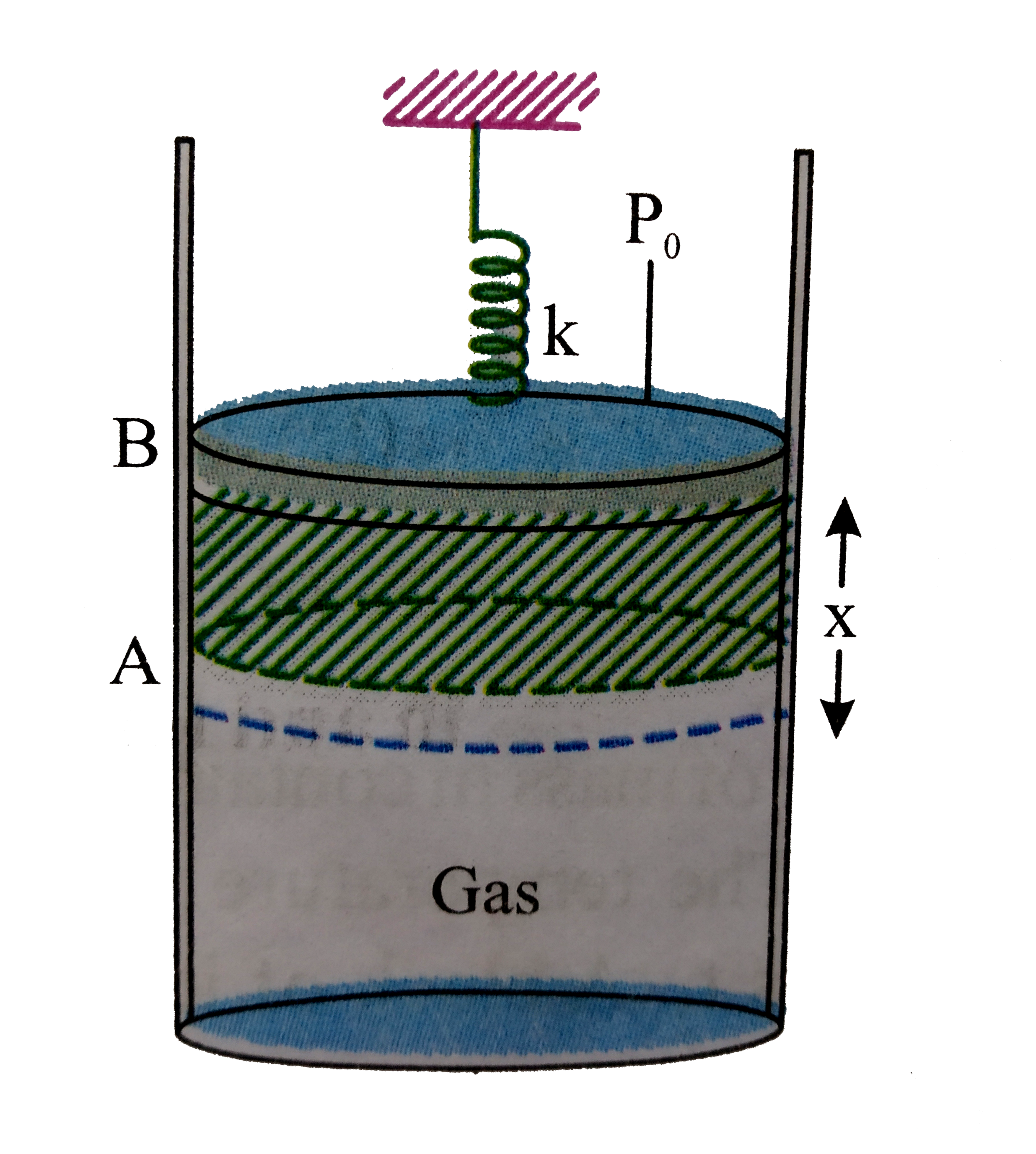
The force constant of spring isA189.6Nm−1B18.96Nm−1C1896Nm−1D2896Nm−1
Two moles of an ideal monoatomic gas are confined within a cylinder by a massless spring loaded with a frictionless piston of negligible mass and of cross-sectional area 4×10−3m2. The springis initially in its relaxed state. Now the gas is heated by a heater for some time. During this time the gas expands and does 50 J of work in moving the piston through a distance of 0.1 m. The temperature of the gas increases by 50 K. Calculate the spring constant and the heat supplied by the heater.
View SolutionAn ideal monatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0×10−3m2. Initially the gas is at 300K and occupies a volume of 2.4×10−3m3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000N/m, atmospheric pressure is 1.0×105Nm−2. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.

View SolutionAn ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0×10−3m2. Initially the gas is at 300K and occupies a volume of 2.4×10−3m3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000N/m, atmospheric pressure is 1.0×105Nm−2. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.

View SolutionAn ideal monoatomic gas is confined in a cylinder by a spring-loaded piston of cross-section 8.0×10−3m2. Initially the gas is at 300K and occupies a volume of 2.4×10−3m3 and the spring is in its relaxed (unstretched, unompressed) state, fig. The gas is heated by a small electric heater until the piston moves out slowly by 0.1m. Calculate the final temperature of the gas and the heat supplied (in joules) by the heater. The force constant of the spring is 8000N/m, atmospheric pressure is 1.0×105Nm−2. The cylinder and the piston are thermally insulated. The piston is massless and there is no friction between the piston and the cylinder. Neglect heat loss through lead wires of the heater. The heat capacity of the heater coil is negligible. Assume the spring to be massless.

View SolutionAn ideal monatonic gas is confined in a cylinder by a spring-loaded piston of cross section 8.0×10−3m2.initially the gas is at 300K and occupies a volume of 2.4×10−3m−3 and the sprinng is in its relaxed state. The gas is heated by a small heater until the piston moves out slowly by 0.1m. Calculate the final tenoerature of the gas. The force constant if the spring is 8000Nm−1,and the atmospheric pressure is 1.0×105Nm−2.Htecyl∈derandtheπs→narethermally∈sylated.Theπs→nandthespr∈garemass≤ssandthereisnoictionbetweentheπs→nandthecyl∈der.Neg≤ctanyheat−lossthroughthe≤adwiresoftheheater.Theheat∩acityoftheheatercoilis¬ligib≤.

View Solution
