कथन-I : θ≠(2n+1)π या (2n+1)π/2,n∈I के किसी वास्तविक मान के लिए व्यंजक y=cos2θ−1cos2θ+cosθ का मान y≤0 या y≥2
क्योंकि
कथन-II : θ के सभी वास्तविक मानों के लिए secθ∈(−∞,−1]∪[1,∞)
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण है।
कथन-I सत्य है, कथन-II सत्य है, कथन-II, कथन-I का सही स्पष्टीकरण नहीं है।
कथन-I सत्य है परन्तु कथन-II असत्य है।
कथन-I असत्य है परन्तु कथन-II सत्य है।
The correct Answer is:D
Step by step video, text & image solution for कथन-I : theta ne (2n+1)pi या (2n+1)pi//2, n in I के किसी वास्तविक मान के लिए व्यंजक y=(cos^(2)theta-1)/(cos^(2)theta+cos theta) का मान y le 0 या y ge 2 क्योंकि कथन-II : theta के सभी वास्तविक मानों के लिए sec theta in (-oo, -1] cup[1,oo) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - ALLEN HINDICHAPTER - त्रिकोणमीतीय समीकरणEXERCISE - EXERCISE-03 MISCELLANEOUS TYPE QUESTIONS (गद्यांश आधारित प्रश्न)3videos
त्रिकोणमीतीय समीकरण
- BOOK - ALLEN HINDICHAPTER - त्रिकोणमीतीय समीकरणEXERCISE - EXERCISE-04 [A] CONCEPTUAL SUBJECTIVE EXERCISE20videos
त्रिकोणमीतीय समीकरण
- BOOK - ALLEN HINDICHAPTER - त्रिकोणमीतीय समीकरणEXERCISE - EXERCISE-03 MISCELLANEOUS TYPE QUESTIONS (स्तम्भ सुमेलन)1videos
त्रिकोणमीतीय समीकरण
- BOOK - ALLEN HINDICHAPTER - त्रिकोणमितीय अनुपात एवं सर्वसमिकायें EXERCISE - EXERCISE - 04 [B] (BRAIN STORMING SUBJECTIVE EXERCISE)11videos
त्रिकोणमितीय अनुपात एवं सर्वसमिकायें
- BOOK - ALLEN HINDICHAPTER - त्रिभुज के हल EXERCISE - DO YOURSELF 101videos
त्रिभुज के हल
Similar Questions
माना S1, समीकरण (1+a)cosθcos(2θ−b)=(1+acos2θ)cos(θ−b) के सभी हलों का समुच्चय है, जो a व b से स्वतंत्र है तथा S2 उन सभी हलों का समुच्चय है जो a व b पर आश्रित है।
उपरोक्त जानकारी के आधार पर, निम्न प्रश्नों के उत्तर दीजिए:
समुच्चय S1 तथा S2 निम्न प्रकार से दिये जायेंगे -02:05View Solutionयदि sinA=sinB तथा cosA=cosB हो, तो A का मान B के पदों में ज्ञात कींजिए।
05:36View Solutionनिम्न प्रश्न में दो स्तम्भ में वक्त्तव्य (statements) दिये हुए हैं जिनका सुमेल (match) करना है। स्तम्भ-I (Column-I) के वक्त्तव्यों को A,B,C तथा D नामित किया गया है जबकि स्तम्भ-II (Column-II) के वक्त्तव्यों को p,q,r तथा s नामित किया गया है। स्तम्भ-I (Column-I) में दिए गए कोई एक वक्त्तव्य स्तम्भ -II (Column-II) के एक वक्त्तव्य से सही सुमेल करता है।
बायीं तरफ समीकरण, अन्त्राल के साथ दी गई है तथा दायीं तरफ हलों की संख्या दी गई है तब सुमेलित कीजिए
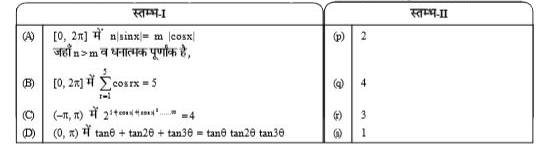View Solutionसिद्ध कीजिए:
न्यूनकोण त्रिभुज ABC में ΣsecA तथा Σtan2A का न्यूनतम मान क्रमश: 6 तथा 9 है।03:18View Solutionएक समबाहु त्रिभुज में, सिद्ध कीजिए कि केन्द्रक और परिवृत्त का केन्द्र (परिकेन्द्र) सम्पाती होते हैं |
05:37View SolutionIf sin3θ+sinθcos2θ=1,thenθ is equal to (n∈Z) (a) 2nπ (b) 2nπ+π2 (c) 2nπ−π2 (d) nπ
View SolutionIf θ∈(π/4,π/2) and ∞∑n=11tannθ=sinθ+cosθ, then the value of tan θ is
03:51View SolutionIf x=∞∑n−0cos2nθ,y=∞∑n=0sin2nθ,z=∞∑n=0cos2nθsin2nθand0<θ<π2, then
05:04View Solution3cosθ+5sin(θ−π6) का θ के किसी भी वास्तविक मान के लिए अधिकतम मान है
02:43View SolutionFor 0 lt theta lt ( pi )/(2) , if x = sum_(n=0)^(oo)cos^(2n) theta, y = sum_(n=0)^(oo) sin^(2n) theta ,z=sum_(n=0)^(oo)cos^(2n) theta sin^(2n) theta ,then :
01:53View SolutionIf x=∞∑n=0cos2nθ,y=∞∑n=θsin2nθandz=∞∑n=0θsin2nθ,0<θ<π2. Then show that xyz=x+y+z.
02:51View SolutionIf x+iy=11−cosθ+2isinθ,θ≠2nπ,n∈I, then maximum value of x is
06:26View SolutionIf θ∈(π/4,π/2) and ∞∑n=11tannθ=sinθ+cosθ, then the value of tan θ is
04:59View SolutionProve that sin^(2n)theta + cos^(2n)theta le 1 for all theta and n ge 1 .
View SolutionIf A=⎡⎢⎣1cosθ1−cosθ1cosθ−1−cosθ1⎤⎥⎦ where 0≤θ≤2π then …..
06:40View Solution