A mass m = 8kg is attached to a spring as shown in figure and held in position so that the spring remains unstretched. The spring constant is 200N/m. The mass m is then released and begins to undergo small oscillations. Find the maximum velocity of the mass (g=10m/s2)
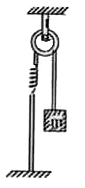
Mean position will be at k , x= mg or x=mgk=8×10200=25=0.4m
This is also the amplitude of oscillation i.e., A= 0.4m
Now vmax=Aω=A√km=(0.4)√2008=2m/s
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE I
184 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE II
175 Videos
- OSCILLATIONSBOOK - AAKASH SERIESCHAPTER - OSCILLATIONSEXERCISE - EXERCISE-3
49 Videos
- OSCILLATIONBOOK - AAKASH SERIESCHAPTER - OSCILLATIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
12 Videos
- PHYSICAL WORLDBOOK - AAKASH SERIESCHAPTER - PHYSICAL WORLDEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
A mass m = 8kg is attached to a spring as shown in figure and held in positioin so that the spring remains unstretched. The spring constant is 200 N/m. The mass m is then released and begins to undergo small oscillations. The maximum velocity of the mass will be (g=10m/s2)
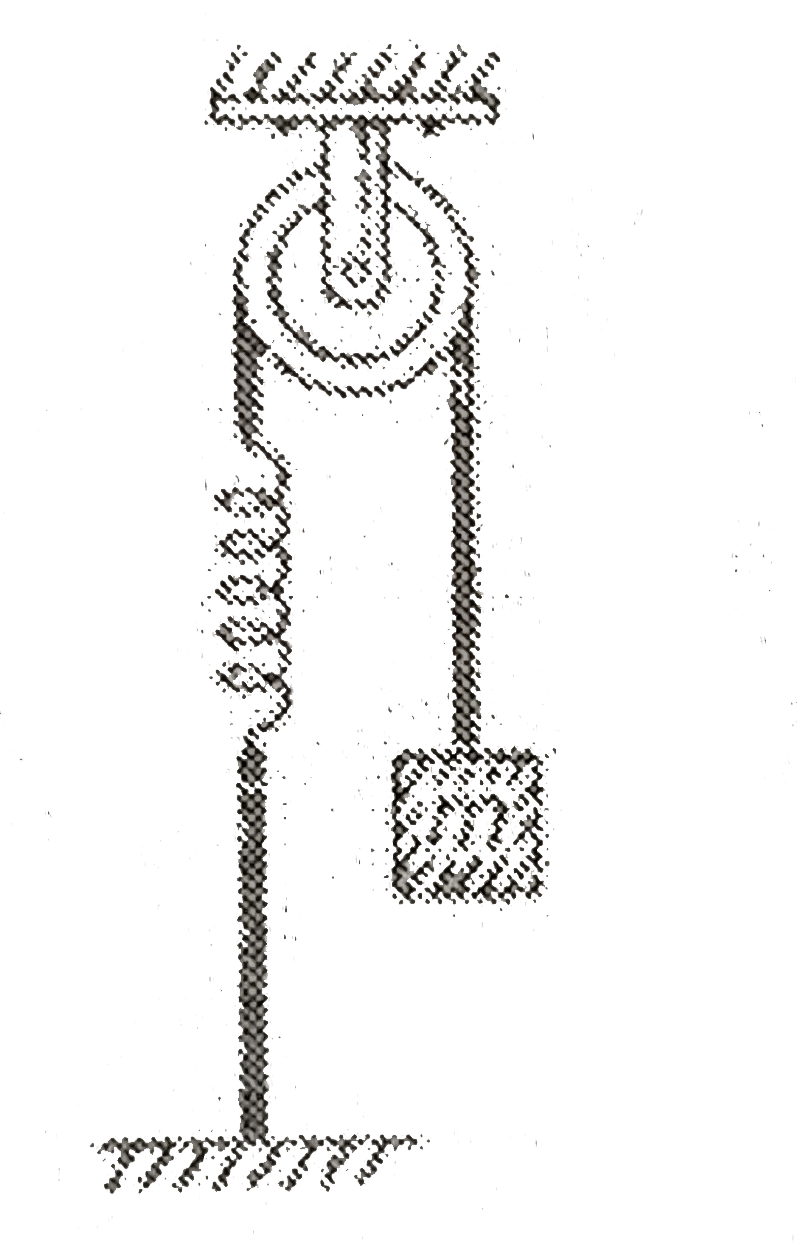
View SolutionA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
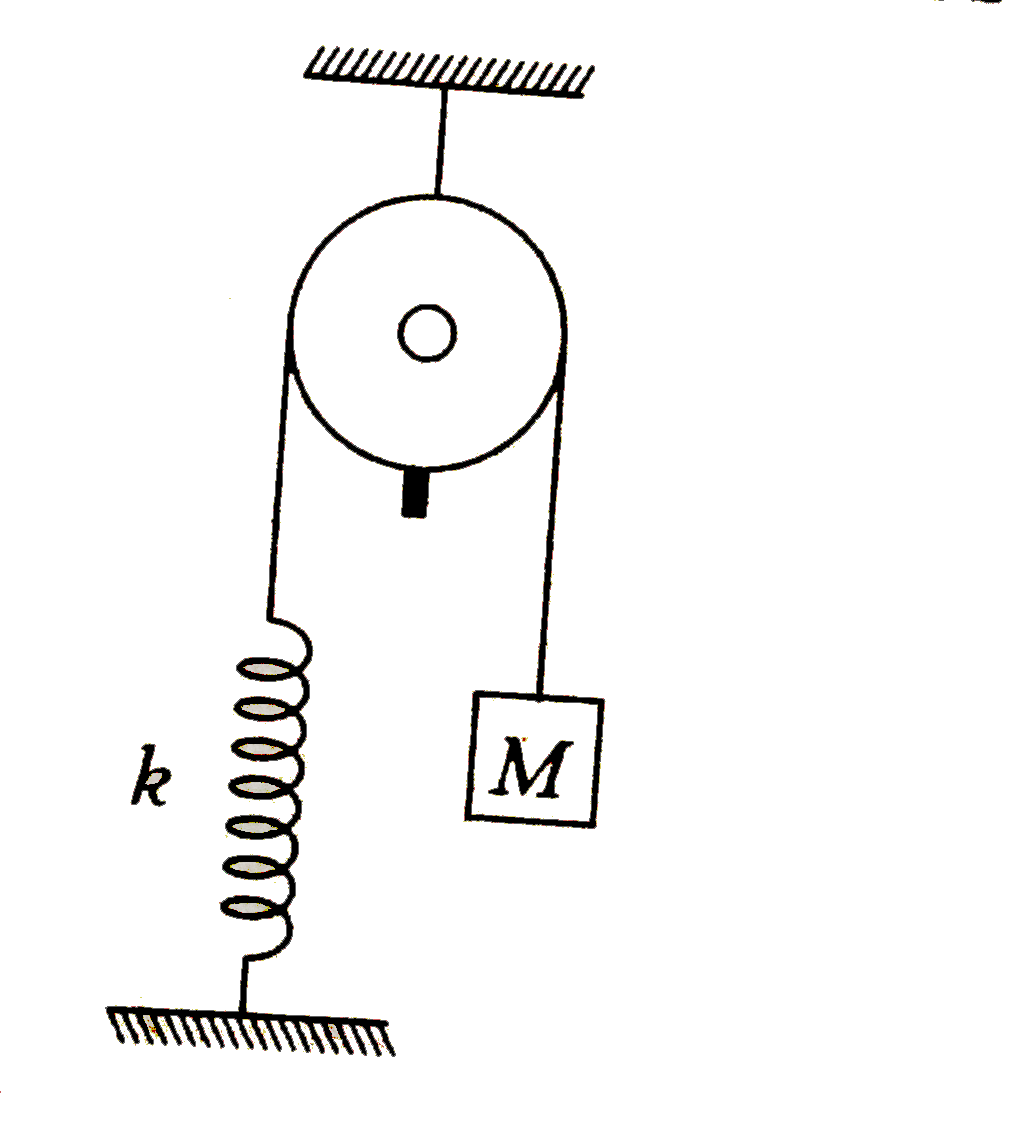
View Solution
Knowledge Check
A mass m=8kg is attached to a spring as shown in figure and held in position so that the spring remains unstretched. The spring constant is 200N/m. The mass m is then released and begins to undergo small oscillations. The maximum velocity of the mass will be (g=10m/s2)
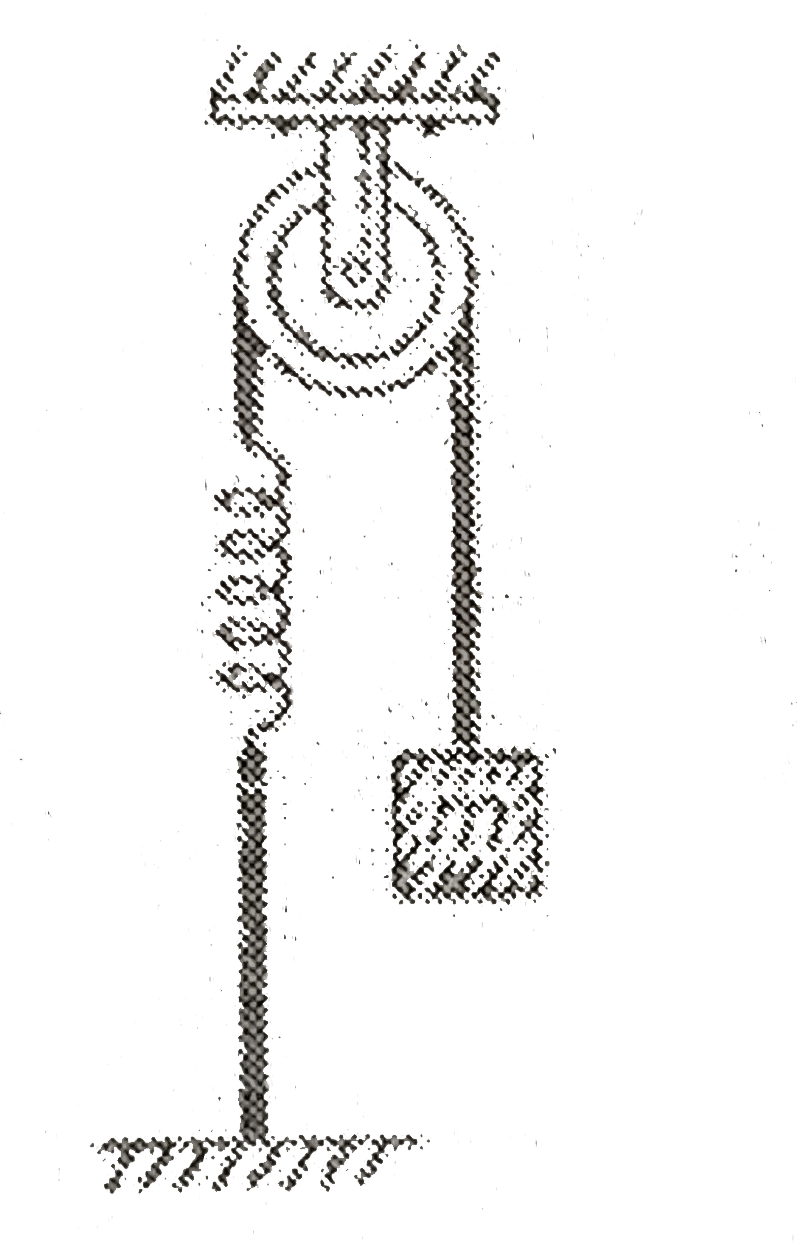 A1 m/sB2 m/sC4 m/sD5 m/s
A1 m/sB2 m/sC4 m/sD5 m/sA mass M=5 kg is attached to a string as shown in the figure and held in position so that the spring remains unstretched. The spring constant is 200Nm−1 . The mass M is then released and begins to undergo small oscillations. The amplitude of oscillation is
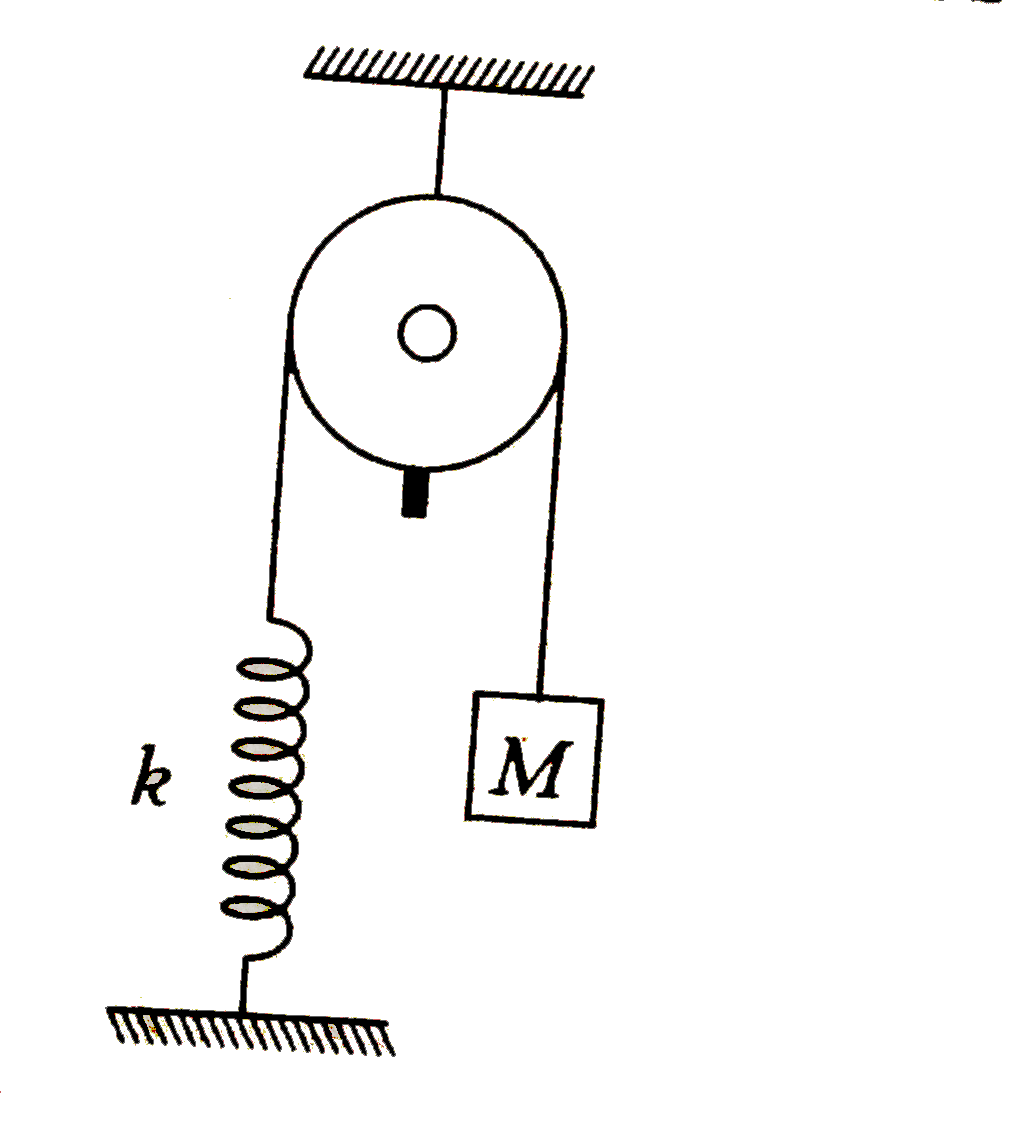 A0.5 mB0.25 mC0.2 mD0.1 m
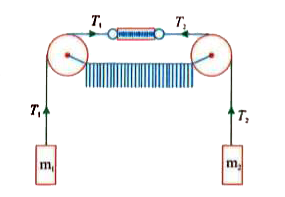
A0.5 mB0.25 mC0.2 mD0.1 mTwo masses m1 and m2 are attached to a spring balance S as shown in figure. m1>m2 then the reading of spring balance will be .
 .A(m1−m2)B(m1+m2)C2m1m2m1+m2Dm1m2m1+m2
.A(m1−m2)B(m1+m2)C2m1m2m1+m2Dm1m2m1+m2
A mass m=8kg is attached to a spring passing over a pulled whose other end is fixed to ground and held in position so that the spring remains unstretched. The spring constant is 200N/m. The mass m is then released and begins to undergo small oscillations. Find maximum velocity of mass
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionThe arranghement shown in the figure below consits of a block of mass 0.1 kg attached to a spring of force cosntant 2×10−3N/M with the help of a pulley so that the spring remians unstretched.On releasing the block , it starts oscillating with a small amplitude . The maximum velocity of block during this motion is close to
View SolutionTwo masses m1 and m2 are attached to a spring balance S as shown in Figure. If m1>m2 then the reading of spring balance will be
View Solution
