An aluminium can of cylindrical shape contains V0cm3 of water. The area of the inner cross-section of the can is A0cm2. ( All measurements refer to T∘0C ). Find the rise in the water level, if the temperature increases to T01(T∘1C>T0).αAIandγwater are given.
V0(T1−T0)(γw−2αAI)A0
V0(T1−T0)(γw−2αAI)2A0
V0(T1−T0)(γw−3αAI)A0
V0(T1−T0)(γw−3αAI)2A0
The correct Answer is:A
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF LIQUIDS (LECTURE SHEET) More than One correct answer Type Questions
2 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF LIQUIDS (LECTURE SHEET) Linked Comprehension Type Questions
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF SOLIDS (PRACTICE SHEET) LEVEL-II (Integer Type Questions)
5 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE
99 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 3
33 Videos
Similar Questions
A aluminium can of cylindrical shape contains 500cm3 of water. The area of the inner cross section of the can is 125cm2. All measurements refer to 10∘C. Find the rise in the water level if the temperature increases to80∘C. The coefficient of linear expansion of aluminium =23×10−6∘C−1 and the average coefficient of volume expansion of water = 3.2×10−4∘C−1 respectively
View SolutionA aluminium can of cylindrical shape contains 500cm3 of water. The area of the inner cross section of the can is 125cm2. All measurements refer ti 10∘C. Find the rise in the water level if the temperature increases to80∘C. The coefficient of linear expansion of aluminium =23×10−6∘C(−1) respectively.
View Solution
Knowledge Check
All the rods have same conductance 'K' and same area of cross section 'A'. If ends A and C are maintained at temperature 2T0 and T0 respectively then which of the following is/are correct?
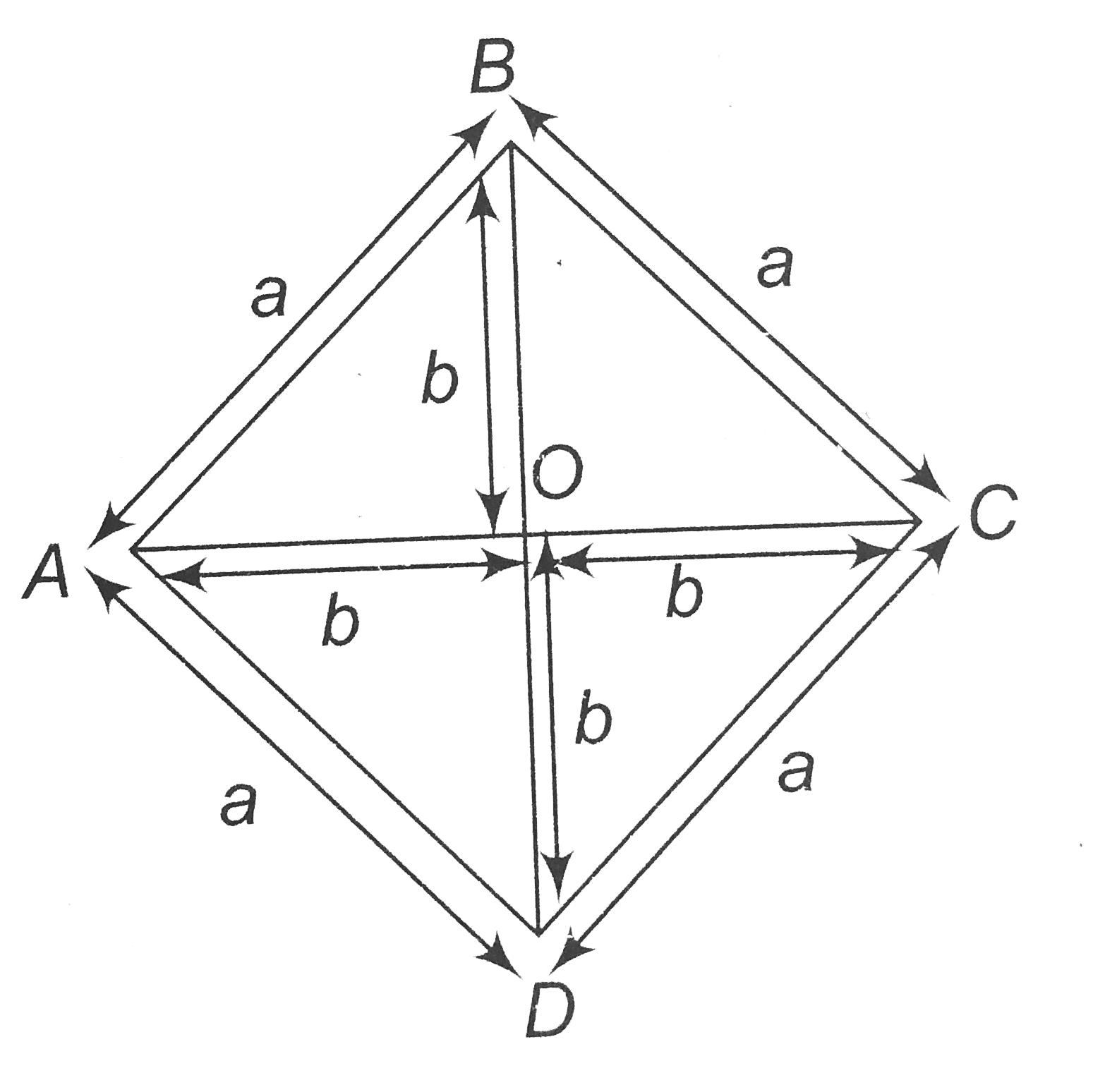 ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are same
ARate of heat flow through ABC,AOCandADC is sameBRate of heat flow through BOandOD is not sameCTotal rate of heat flow from A to C is 3KAT02aDTemperature at junctions B,OandD are sameThe quantity of heat which can rise the temperature of xgm of a substance through t∘1C can rise the temperature of ygm of water through t∘2C is same. The ratio of specific heats of the substances is
Ayt1/xt2Bxt2/yt1Cyt2/xt1Dxt1/yt2
A aluminum can of cylindrical shape contains 500cm3 of water. The area of the inner cross section of the can is 125cm2. All measurements refer to 10∘C. Find the rise in the water level if the temperature increases to80∘C. The coefficient of linear expansion of aluminum =23×10−6C−1 and the average coefficient of volume expansion of water=3.2×10−4C−1 respectively.
View SolutionThe density of water at 0∘C is 0.998gcm−3 at 4∘C is 1.00gcm−3. Calculate the average coefficient of volume expansion of water in the temperature range 0∘C to 4∘C.
View SolutionAll the rods have same conductance 'K' and same area of cross section 'A'. If ends A and C are maintained at temperature 2T0 and T0 respectively then which of the following is/are correct?

View SolutionA monatomic ideal gas is contained in a rigid container of volume V with walls of total inner surface area A, thickness x and thermal conductivity K. The gas is at an initial temperature t0 and pressure P0 . Find the pressure of the gas as a function of time if the temperature of the surrounding air is Ts . All temperature are in absolute scale.
View SolutionAt the mount of the tap area of cross-section is 2.0cm2 and the speed of water is 3m/s. The area of cross-section of the water column 80 cm below the tap is (use g=10m/s2)
View SolutionA cylindrical object of the :uea of cross section 5 cm2 fl.oatS (lateral side vertical) in water filled in a cylindrical container of the area of cross section 15 cm2 When the object is placed in water the level of the water in the comainer rises by 2 cm and the len
View Solution
