Passage - II :
Liquids do not have definite shape and size, they are taken in a vessel. Their expansion (or) contraction takes place with respect to the container in which they arc considered. The volume coefficient of expansion relative to the vessel is termed as coefficient of apparent expansion $(γ_{a})$ and the volume coefficient of expansion of the liquid is termed as absolute $(γ_{R} or γ_{L})$ . In some of the arrangements mentioned as per the instructions. solve the problems.
A metallic scale reads correct values at 0°C. It registers the height of liquid in the vessel (cylindrical shape) at 0°C as $h_{0}$ . If $γ_{C}, γ_{L}$ are the coefficients of cubical expansion of metallic scale and liquid respectively and $α_{S}$ is the coefficient of linear expansion of the material of the cylindrical vessel made of material different to that of the scale, then the scale reading. Registering the height of the liquid in the vessel as function of temperature $(θ)$ of the surroundings is

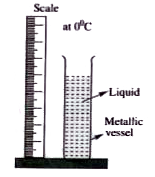
$h_{θ} = h_{0} [1 - (γ_{C} - γ_{L} - 2 α_{S}) θ]$

$h_{θ} = h_{0} [1 - (γ_{C} - γ_{L} + 2 α_{s}) θ]$

$h_{θ} = h_{0} [1 - (γ_{C} - γ_{L} + α_{S}) θ]$

$h_{θ} = h_{0} [1 - (γ_{C} - γ_{L} - α_{S}) θ]$

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

The superficial coefficient of expansion $β$ and volume coefficient of expansion $γ$ are related as
A $γ = 2 β$
B $γ = 3 β$
C $γ = \frac{3}{2} β$
D $γ = β$
The absolute coefficient of expansion of a liquid is 7 times that the volume coefficient of expansion of the vessel. Then the ratio of absolute and apparent expansion of the liquid is
A $\frac{1}{7}$
B $\frac{7}{6}$
C $\frac{6}{7}$
Dnone of these
The coefficient of real expansion of liquid is $γ_{R}$ and the coefficient of appareent expansion of the liquid is $γ_{A}$ . The coefficient of cubical expansion of the vessel is $γ$ . If $γ_{R} : γ_{A} = 4 : 1$ then $γ_{A} : γ$ is
A $3 : 1$
B $1 : 3$
C $4 : 1$
D $1 : 4$