Suppose that on early morning when the themperature is 100∘C, a driver of an automobile gets his gasoline tank which is made of steel, filled with 75 litre of gasoline, which is also at 10∘ C. During the day, the temperature rises to 30∘ C. How much gasoline will overflow? Given α for steel =1.2×10−5/∘Candγ for gasoline =9.5×10−4/∘C.
The correct Answer is:1.37 litre
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF GASES (LECTURE SHEET) Straight Objective Type Questions (Ideal Gas equation - applications)
10 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF GASES (LECTURE SHEET) Straight Objective Type Questions (Boyle.s Law - applications)
5 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH SERIESCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXPANSION OF LIQUIDS (PRACTICE SHEET) LEVEL-II (Matrix Matching Type Questions)
3 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH SERIESCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE
99 Videos
- THERMODYNAMICSBOOK - AAKASH SERIESCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE - 3
33 Videos
Similar Questions
Assume that one early morning when the temperature is 10∘C a driver of an automobile gets his gasoline tank which is made of steel, filled with 75 L of gasoline, which is also at 10∘C Durign the day, the temperature rises at 30∘C how much gasoline will overflow ?
(Given, α for steel = 1.2×10−5∘C−1,γ for gasoline =9.5×10−4∘C)
View SolutionAssume that one early morning when the temperature is 10∘C a driver of an automobile gets his gasoline tank which is made of steel, filled with 75 L of gasoline, which is also at 10∘C Durign the day, the temperature rises at 30∘C how much gasoline will overflow ?
(Given, α for steel = 1.2×10−5∘C−1,γ for gasoline =9.5×10−4∘C)
View Solution
Knowledge Check
A steel metre scale is to be ruled so that the millimetre intervals are accurate to within about 5×10−5mm at a certain temperature. What is the maximum temperature variation allowable during the ruling ? Given α for steel =1.1×10−5.∘C−1.
A8∘CB9∘CC4.5∘CD10∘C
Assume that one early morning when the temperatures in 10∘C, a driver of an automobile gets his gasoline tank which is made of steel, tilled with 75 L of gasoline, which is also at 10∘C. During the day, the tempaerature rises to 30∘C, how much gasoline will overflow ?
(Given, α for steel =1.2×10−5∘C^1,γ for gasoline
=9.5×10−4∘C−1)
View SolutionThe driver of an automobile gets his steel gasoline tank filled with 50 ltrs of gasoline at surrounding temperature of 20∘C . At afternoon, the temperature rises to 40∘C . How much of the gasoline will overflow? Coefficient of linear expansion for steel , αs=1.3×10−5∘C−1 and for gasoline γg=9.4×10−4∘C−1
View SolutionA gasoline tank made of steel is filled completely with 60 litres of gasoline, both at a temperature of 12∘C . How much gasoline will overflow when the temperature is increased to 25∘C ?
αsteel=1.1×10−5∘C−1
γgasoline=9.5×10−4∘C−1
View SolutionA steel metre scale is to be ruled so that the millimetre intervals are accurate to within about 5×10−5mm at a certain temperature. What is the maximum temperature variation allowable during the rulting ? Given α for steel =1.1×10−5.∘C−1.
View SolutionTwo metre scales, one of steel and the other of aluminium, agree at 20C. Calculate the ratio aluminium-centimetre/steel-centimeter at (a) 0C, (b) 40C and (c) 100C. αforsteel=1.1×10−5oC(−1)andforaluminium=2.3 xx 10^(-5) 0^C(-1).
View SolutionA rail track made of steel having length 10 m is clamped on a railway line at its two ends
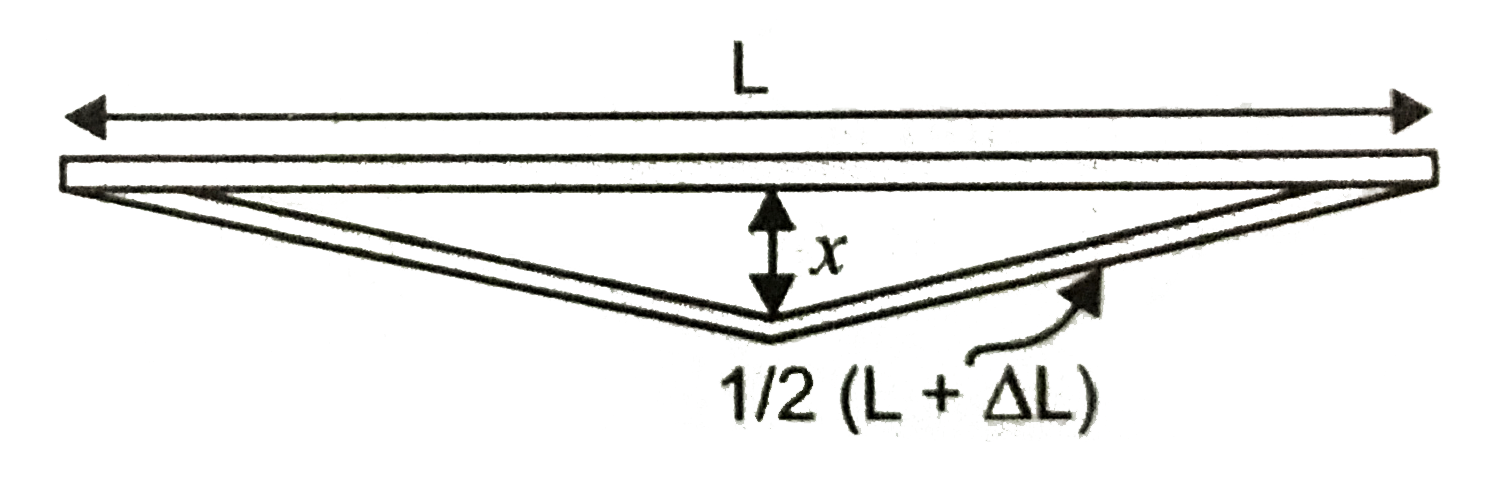
on a summer day due to rise in temperature by 20∘C, it is deformed as shown in fig. Find x (displacement of the centre) if αsteel=1.2×10−5/∘C.
View SolutionA rail track made of steel having length 10 m is clamped on a railway line at its two ends

on a summer day due to rise in temperature by 20∘C, it is deformed as shown in fig. Find x (displacement of the centre) if αsteel=1.2×10−5/∘C.
View Solution
