An infinitely long wire carrying a current i is bent at its mid point 0 to form an angle 45∘. P is point a distance Rfrom the pointofbending. Find the magnetic field at P.

Since point P lies on the axis of straight part OA, magnetic field at point P is zero due to path OA of wire
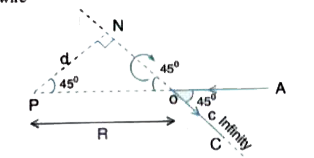
From ΔOPN,d=Rcos450
Since both the ends O and C are on the same side of normal PN,
ϕ1=−450andϕ2=+900
So B=μ0i4πd(sinϕ1+sinϕ2)
=μ0i4πRcos450[sin(−450)+sin900]
=μ0i×√24πR(−sin45∘+1),=√μ0i4πR(1−1√2)⊗
=(√2−1)μ0i4πR⊗ (into the page)
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS )
18 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -I)
30 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
20 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
4 Videos
Similar Questions
A long straight wire, carrying current I, is bent at its midpoint to form an angle of 45∘. Find the induction of magnetic field at point P, distant R from the point of bending (as shown in)

View SolutionA long straight wire, carrying current I, is bent at its midpoint to form an angle of 45∘. Find the induction of magnetic field at point P, distant R from the point of bending (as shown in)

View Solution
Knowledge Check
A long straight wire, carrying current I, is bent at its midpoint to form an angle of 45∘. Find the induction of magnetic field at point P, distant R from the point of bending (as shown in)
 A(√2−1)μ0i4πRB(√2+1)μ0i4πRCμ0i4√3πRDμ0i8R
A(√2−1)μ0i4πRB(√2+1)μ0i4πRCμ0i4√3πRDμ0i8RA long wire carrying a current i is bent to form a plane angle. The magnitude of magnetic field at height d, above the point of bending
A√2μ0i4πdB3√2μ0i4πdC5√2μ0i4πdD7√2μ0i4πdAn infinitely long wire carrying current I is along Y-axis such taht its one end is at point A(0,b) while the wire extends upto +∞. The magnitude of magnetic field strength at point (a,0) is
 Aμ0I4πa(1+b√a2+b2)Bμ0I4πa(1−b√a2+b2)Cμ0I4πa(b√a2+b2)Dnone of these
Aμ0I4πa(1+b√a2+b2)Bμ0I4πa(1−b√a2+b2)Cμ0I4πa(b√a2+b2)Dnone of these
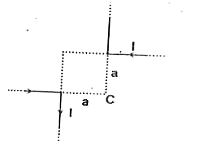
Two inflinitely long wires carrying current I, are bent as shown in the figure. Find the magnetic induction at point C.
View SolutionAn infinitely long wire carrying current I is along Y-axis such taht its one end is at point A(0,b) while the wire extends upto +∞. The magnitude of magnetic field strength at point (a,0) is

View SolutionAn infinitely long wire carrying current I is along Y-axis such taht its one end is at point A(0,b) while the wire extends upto +∞. The magnitude of magnetic field strength at point (a,0) is

View SolutionAn infinitely long wire carrying current I is along Y-axis such taht its one end is at point A(0,b) while the wire extends upto +∞. The magnitude of magnetic field strength at point (a,0) is

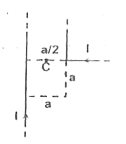
View Solutionone of the two infinitely long wires carrying current I is bent as shown in the adjacent figure. The magnetic induction at C is equal to
View Solution
